摘要: (2011湖南湘潭市.26.10分) 已知.AB是⊙O的直径.AB=8.点C在⊙O的半径OA上运动.PC⊥AB.垂足为C.PC=5.PT为⊙O的切线.切点为T. ⑴ 如图⑴.当C点运动到O点时.求PT的长; ⑵ 如图⑵.当C点运动到A点时.连结PO.BT.求证:PO∥BT; ⑶ 如图⑶.设..求与的函数关系式及的最小值. [答案]解:(1)连接OT. 当C点运动到O点时.∵PT为⊙O的切线.∴OT⊥PT, ∴在Rt△PTO中.. (2)连接AT, 当C点运动到A点时.∵PC⊥AB.∴PA是⊙O的切线. ∵PT为⊙O的切线.∴PA=PT.PO平分∠APT.∴PO⊥AT. ∵AB是⊙O的直径.∴∠ATB是直角.即BT⊥AT.∴PO∥BT. ⑶连接OP.OT.∵.∴. ∵在Rt△PCO中. 在Rt△POT中., ∴.即. ∴. 当x=4时.y最小其值为9. ∴与的函数关系式为. 的最小值是9.
网址:http://m.1010jiajiao.com/timu3_id_496435[举报]
(1)如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且AB=26m,OE⊥CD于点E.水位正常时测得OE:CD=5:24,求CD的长;

(2)如图,已知:AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC.求证:DE是⊙O的切线.

查看习题详情和答案>>

(2)如图,已知:AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC.求证:DE是⊙O的切线.

 20、已知:AB是⊙O的弦,OD⊥AB于M交⊙O于点D,CB⊥AB交AD的延长线于C.
20、已知:AB是⊙O的弦,OD⊥AB于M交⊙O于点D,CB⊥AB交AD的延长线于C.(1)求证:AD=DC;
(2)过D作⊙O的切线交BC于E,若DE=2,CE=1,求⊙O的半径.
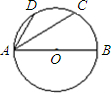 如图,已知:AB是⊙O的直径,∠BAC=32°,D是
如图,已知:AB是⊙O的直径,∠BAC=32°,D是
 如图,已知:AB是⊙O的直径,弦CD⊥AB于H,CE平分∠DCO交⊙O于点E.
如图,已知:AB是⊙O的直径,弦CD⊥AB于H,CE平分∠DCO交⊙O于点E.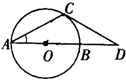 27、如图,已知:AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=5.
27、如图,已知:AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=5.