0 47924 47932 47938 47942 47948 47950 47954 47960 47962 47968 47974 47978 47980 47984 47990 47992 47998 48002 48004 48008 48010 48014 48016 48018 48019 48020 48022 48023 48024 48026 48028 48032 48034 48038 48040 48044 48050 48052 48058 48062 48064 48068 48074 48080 48082 48088 48092 48094 48100 48104 48110 48118 447348

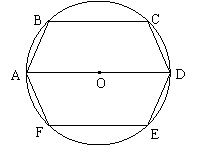 (1)当∠BAD=75°时,求的长;
(1)当∠BAD=75°时,求的长;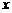 ,求六边形ABCDEF的周长L关于
,求六边形ABCDEF的周长L关于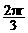 .··························································································· (3分)
.··························································································· (3分)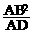 =
=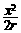 ,∴BC=2r-
,∴BC=2r-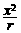 ,同理EF=2r-
,同理EF=2r-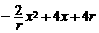 =
=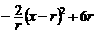 ,其中0<x<
,其中0<x<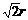 ·········· (9分)
·········· (9分) (长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;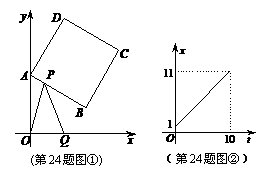 (3) 在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.
(3) 在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.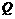 (1,0)
-----------------------------1分
(1,0)
-----------------------------1分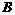 作BF⊥y轴于点
作BF⊥y轴于点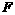 ,
,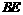 ⊥
⊥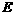 ,则
,则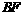 =8,
=8,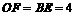 .
.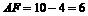 .
.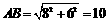 .----------------------------5分
.----------------------------5分 过点
过点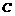 作
作 ⊥
⊥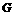 ,与
,与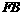 的延长线交于点
的延长线交于点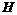 .
.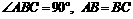 ∴△ABF≌△BCH.
∴△ABF≌△BCH.
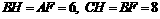 .
. 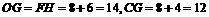 .
.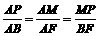 .
. 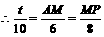 .
. 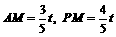 . ∴
. ∴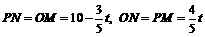 .
.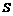 (平方单位)
(平方单位) (0≤
(0≤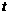 ≤10) ------------------10分
≤10) ------------------10分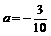 <0 ∴当
<0 ∴当 时, △OPQ的面积最大.------------11分
时, △OPQ的面积最大.------------11分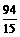 ,
,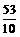 ) .
---------------------------------12分
) .
---------------------------------12分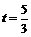 或
或 时, OP与PQ相等.---------------------------14分
时, OP与PQ相等.---------------------------14分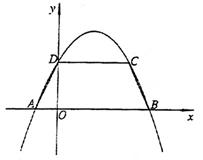
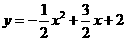 ;⑵
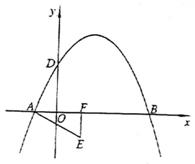
;⑵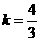 ;⑶M(3,2),N(1,3)
;⑶M(3,2),N(1,3)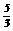 个单位长度的速度向终点B运动.设运动了x秒.
个单位长度的速度向终点B运动.设运动了x秒.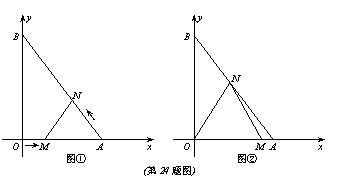
 (1)求折痕EF的长;
(1)求折痕EF的长;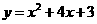 的顶点?若存在,求出t值;若不存在,请说明理由;
的顶点?若存在,求出t值;若不存在,请说明理由;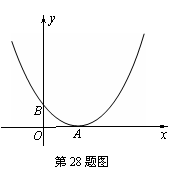
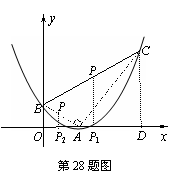
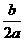 ,0),
,0),
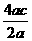 =2c=2.∴A(2,0). ………………………………………2分
=2c=2.∴A(2,0). ………………………………………2分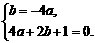 解得a =
解得a =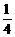 ,b =-1.
,b =-1. 另解: 由抛物线过B(0,1) 得c=1.又b2-4ac=0, b=-4ac,∴b=-1. ………2分
另解: 由抛物线过B(0,1) 得c=1.又b2-4ac=0, b=-4ac,∴b=-1. ………2分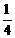 ,故y=
,故y=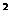 -x+1.
……………………………………………4分
-x+1.
……………………………………………4分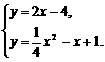 解得x1=10,x2=2.
解得x1=10,x2=2.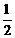 (OB+CD)=
(OB+CD)=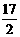 .∵D (10,0), ∴P1 (5,0), ∴P (5,
.∵D (10,0), ∴P1 (5,0), ∴P (5, 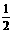 .∵A (2,0), ∴P2(1,0), ∴P (1,
.∵A (2,0), ∴P2(1,0), ∴P (1,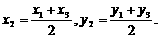 ………………………………………12分
………………………………………12分

 5分
5分 BC=1
BC=1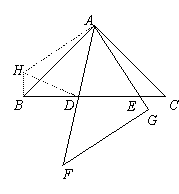 ∠ABH=∠C=45°,旋转角∠EAH=90°.
∠ABH=∠C=45°,旋转角∠EAH=90°.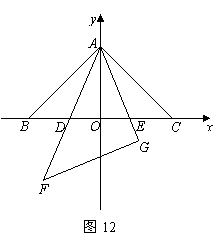
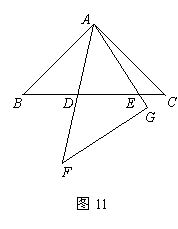 (4)在旋转过程中,(3)中的等量关系BD
(4)在旋转过程中,(3)中的等量关系BD