0 47983 47991 47997 48001 48007 48009 48013 48019 48021 48027 48033 48037 48039 48043 48049 48051 48057 48061 48063 48067 48069 48073 48075 48077 48078 48079 48081 48082 48083 48085 48087 48091 48093 48097 48099 48103 48109 48111 48117 48121 48123 48127 48133 48139 48141 48147 48151 48153 48159 48163 48169 48177 447348
 B.
B.
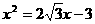 D.
D.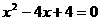
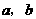 是方程
是方程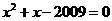 的两个实数根,则
的两个实数根,则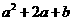 的值为( )
的值为( )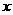 的一元二次方程
的一元二次方程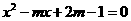 的两个实数根分别是
的两个实数根分别是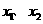 ,且
,且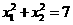 ,则
,则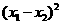 的值是( )
的值是( )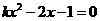 有两个不相等的实数根,则
有两个不相等的实数根,则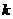 的取值范围是( )
的取值范围是( )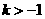 B.
B.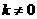 C.
C.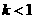 D.
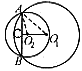
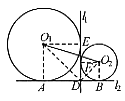
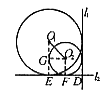
D. 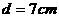 ,小圆的半径
,小圆的半径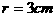 ,求大圆的半径。
,求大圆的半径。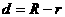 ,得
,得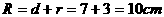 。
。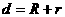 ,得
,得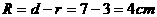 。
。

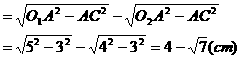
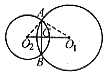

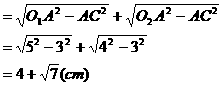
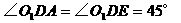 ,
,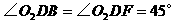 ,
,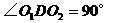 ,
,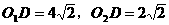 。
。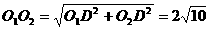 。
。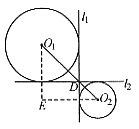
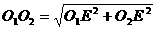
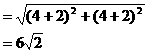
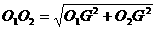
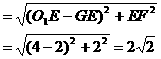
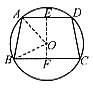
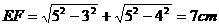 ,
,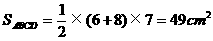 。
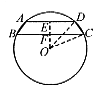
。
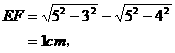
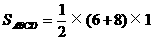
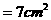 。
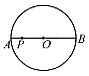
。
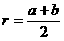 ;
;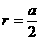 ;
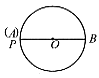
;
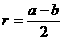 。
。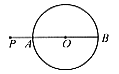
 (3)若给定a=6,试判定直线AP与⊙C的位置关系(要求说明理由)。
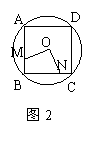
(3)若给定a=6,试判定直线AP与⊙C的位置关系(要求说明理由)。 如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连结OM、ON。
如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连结OM、ON。