摘要: 解:(1)∆ABE∽∆DAE, ∆ABE∽∆DCA 1分 ∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45° ∴∠BAE=∠CDA 又∠B=∠C=45° ∴∆ABE∽∆DCA 3分 (2)∵∆ABE∽∆DCA ∴ 由依题意可知CA=BA= ∴ ∴m= 5分 自变量n的取值范围为1<n<2. 6分 (3)由BD=CE可得BE=CD,即m=n ∵m= ∴m=n= ∵OB=OC=BC=1 ∴OE=OD=-1 ∴D(1-, 0) 7分 ∴BD=OB-OD=1-(-1)=2-=CE, DE=BC-2BD=2-2(2-)=2-2 ∵BD+CE=2 BD=2(2-)=12-8, DE=(2-2)= 12-8 ∴BD+CE=DE 8分 (4)成立 9分 证明:如图,将∆ACE绕点A顺时针旋转90°至∆ABH的位置,则CE=HB,AE=AH, ∠ABH=∠C=45°,旋转角∠EAH=90°. 连接HD,在∆EAD和∆HAD中 ∵AE=AH, ∠HAD=∠EAH-∠FAG=45°=∠EAD, AD=AD. ∴∆EAD≌∆HAD ∴DH=DE 又∠HBD=∠ABH+∠ABD=90° ∴BD+HB=DH 即BD+CE=DE 12分
网址:http://m.1010jiajiao.com/timu3_id_480213[举报]
 22、推理说明题
22、推理说明题已知:如图,AB∥CD,∠A=∠D,试说明AC∥DE成立的理由.下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.
解:∵AB∥CD (已知)
∴∠A=
∠ACD
(两直线平行,内错角相等)又∵∠A=∠D (
已知
)∴∠
ACD
=∠D
(等量代换)∴AC∥DE (
内错角相等,两直线平行
) 23、已知:如图,AB∥CD,∠A=∠D,试说明 AC∥DE 成立的理由.
23、已知:如图,AB∥CD,∠A=∠D,试说明 AC∥DE 成立的理由.(下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.)
解:∵AB∥CD (已知)
∴∠A=
∠ACD
(两直线平行,内错角相等)又∵∠A=∠D(
已知
)∴∠
ACD
=∠D
(等量代换)∴AC∥DE (
内错角相等,两直线平行
) 推理说明题
推理说明题(1)已知:如图1,AB∥CD,∠A=∠D,试说明 AC∥DE 成立的理由.
下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.
解:∵AB∥CD (已知)
∴∠A=
∠ACD
∠ACD
(两直线平行,内错角相等)又∵∠A=∠D
(已知),
(已知),
∴∠
ACD
ACD
=∠D
D
(等量代换)∴AC∥DE
(内错角相等,两直线平行).
(内错角相等,两直线平行).
(2)如图2:已知∠1=∠2,∠3=115°,求∠4的度数.
 22、如图,已知AB是∠DAC的角平分线,∠C=∠D.请将下面说明AC=AD的过程和理由补充完整:
22、如图,已知AB是∠DAC的角平分线,∠C=∠D.请将下面说明AC=AD的过程和理由补充完整: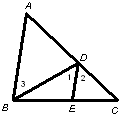 27、如图,∠A=∠3=55°,AB∥DE,求∠1、∠2的度数.
27、如图,∠A=∠3=55°,AB∥DE,求∠1、∠2的度数.