摘要:24.(本小题满分12分)如图①.在平面直角坐标系中.A点坐标为(3.0).B点坐标为(0.4).动点M从点O出发.沿OA方向以每秒1个单位长度的速度向终点A运动,同时.动点N从点A出发沿AB方向以每秒个单位长度的速度向终点B运动.设运动了x秒. (1)点N的坐标为( . ),(用含x的代数式表示) (2)当x为何值时.△AMN为等腰三角形? (3)如图②.连结ON得△OMN.△OMN可能为正三角形吗?若不能.点M的运动速度不变.试改变点N的运动速度.使△OMN为正三角形.并求出点N的运动速度和此时x的值.
网址:http://m.1010jiajiao.com/timu3_id_480216[举报]
18、如图,在平面直角坐标系中,已知点A(-4,0),B(0,3),对△AOB连续作旋转变换,依次得到三角形(1),(2),(3),(4),…,那么第(7)个三角形的直角顶点的坐标是

查看习题详情和答案>>
(24,0)
,第(2011)个三角形的直角顶点坐标是(8040,0)
.
 已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).(1)求直线l1,l2的表达式;
(2)点C为l1上一动点,作CD∥y轴交直线l2于点D,线段CD长度为6,求点C的坐标.
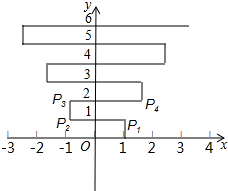 如图,在平面直角坐标系上有个点P(1,0),点P第一次向上跳动1个单位至P1(1,1),紧接着第二次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第一次向上跳动1个单位至P1(1,1),紧接着第二次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是( )
查看习题详情和答案>>
(2010•广阳区二模)如图,在平面直角坐标系中,已知点A(0,16),D(24,0),点B在第一象限,且AB∥x轴,BD=20,动点P从原点O开始沿y轴正半轴以每秒4个单位长的速度向点A匀速运动,过点P作x轴的平行线与BD交于点C;动点Q从点A开始沿线段AB-BD以每秒8个单位长的速度向点D匀速运动,设点P、Q同时开始运动且时间为t(t>0),当点P与点A重合时停止运动,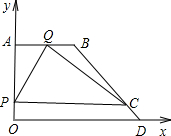 点Q也随之停止运动.
点Q也随之停止运动.
(1)求点B的坐标及BD所在直线的解析式;
(2)当t为何值时,点Q和点C重合?
(3)当点Q在AB上(包括点B)运动时,求S△PQC与t的函数关系式;
(4)若∠PQC=90°时,求t的值.
查看习题详情和答案>>
 点Q也随之停止运动.
点Q也随之停止运动.(1)求点B的坐标及BD所在直线的解析式;
(2)当t为何值时,点Q和点C重合?
(3)当点Q在AB上(包括点B)运动时,求S△PQC与t的函数关系式;
(4)若∠PQC=90°时,求t的值.
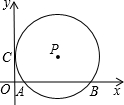 如图,在平面直角坐标系中,⊙P与y轴相切于点C,与x轴相交于A,B两点,若点P的坐标为(5,3),点M是⊙P上的一动点,则△ABM面积的最大值为( )
如图,在平面直角坐标系中,⊙P与y轴相切于点C,与x轴相交于A,B两点,若点P的坐标为(5,3),点M是⊙P上的一动点,则△ABM面积的最大值为( )