0 47922 47930 47936 47940 47946 47948 47952 47958 47960 47966 47972 47976 47978 47982 47988 47990 47996 48000 48002 48006 48008 48012 48014 48016 48017 48018 48020 48021 48022 48024 48026 48030 48032 48036 48038 48042 48048 48050 48056 48060 48062 48066 48072 48078 48080 48086 48090 48092 48098 48102 48108 48116 447348
 (10分)解:(1)设抛物线的表达式为
(10分)解:(1)设抛物线的表达式为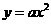 1分
1分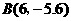 在抛物线的图象上.
在抛物线的图象上.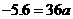
 ······························································ 3分
······························································ 3分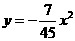 ············································································· 4分
············································································· 4分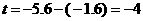 ··························································· 5分
··························································· 5分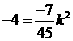
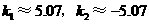 (舍去)············································································ 6分
(舍去)············································································ 6分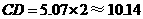 (m)·············································································· 7分
(m)·············································································· 7分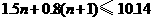 ····················································································· 9分
····················································································· 9分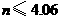 .
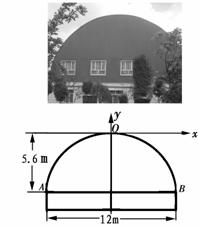
.
 的边
的边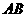 在
在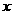 轴上,且
轴上,且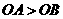 ,以
,以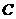 .若点
.若点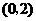 ,
,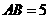 ,A、B两点的横坐标
,A、B两点的横坐标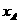 ,
,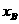 是关于
是关于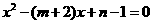 的两根.
的两根. 、
、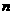 的值;
的值; 平分线所在的直线
平分线所在的直线 交
交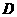 ,试求直线
,试求直线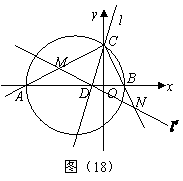 (3)过点
(3)过点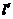 分别交射线
分别交射线 、
、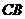 (点
(点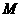 、
、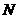 .则
.则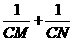 的是否为定值?若是,求出该定值;若不是,请说明理由.
的是否为定值?若是,求出该定值;若不是,请说明理由. 以
以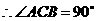 ,而点
,而点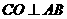 易知
易知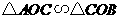 ,
,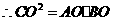 ,····································································································· 1分
,····································································································· 1分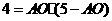 ,解之得:
,解之得: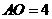 或
或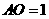 .
. ,
,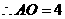 ,
,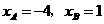 .···································································································· 2分
.···································································································· 2分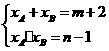 ,
,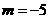 ,
,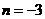 .································································································ 4分
.································································································ 4分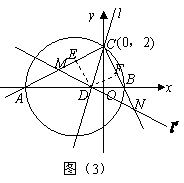 (2)如图(3),过点
(2)如图(3),过点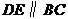 ,交
,交 于点
于点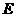 ,
,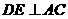 ,且
,且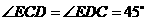 ,
,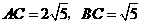 ,··········· 5分
,··········· 5分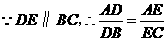 ,
,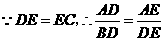 ,
, ,有
,有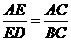 ,
,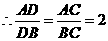 ,······································································································· 6分
,······································································································· 6分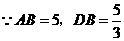 ,
,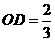 ,即
,即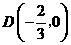 ,························································································ 7分
,························································································ 7分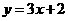 .··················································· 8分
.··················································· 8分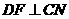 于
于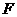 ,
,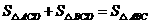 ,
,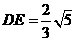 .········································································································ 5分
.········································································································ 5分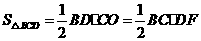 ,
,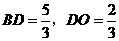 .····························································································· 7分
.····························································································· 7分 为
为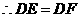 .
. ,有
,有 ········································································· 9分
········································································· 9分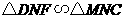 ,有
,有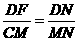 ······································································ 10分
······································································ 10分 ,··············································································· 11分
,··············································································· 11分  .···················································································· 12分
.···················································································· 12分 角的直角三角板
角的直角三角板 (
(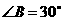 )绕其直角顶点
)绕其直角顶点 逆时针旋转
逆时针旋转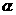 解(
解(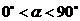 ),得到
),得到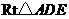 ,
,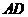 与
与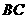 相交于点
相交于点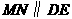 交
交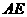 于点
于点 .设
.设 ,
, 的面积为
的面积为 ,
, .
.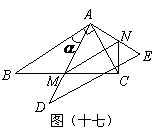 (1)求证:
(1)求证: ,
,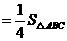 时,试判断直线
时,试判断直线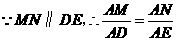 ,
,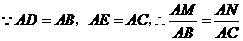 ,································································· 1分
,································································· 1分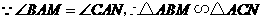 ,···························································· 2分
,···························································· 2分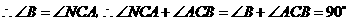 ,
, ,即
,即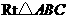 中,
中,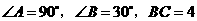 ,
,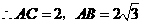 ,
,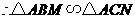 ,
,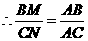 ,
,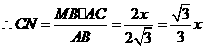 ;··············································································· 4分
;··············································································· 4分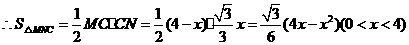 ;··························· 5分
;··························· 5分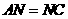 .
.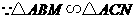 ,
, .
.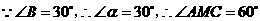 ,································································· 6分
,································································· 6分 ,
,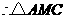 是等边三角形,
是等边三角形,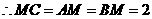 ,
,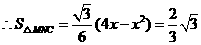 ,
,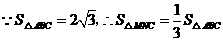 ;······································································ 7分
;······································································ 7分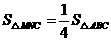 时,
时,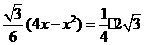 ,解之得
,解之得 或
或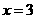 ;··················································· 8分
;··················································· 8分 ,
, 中,
中,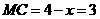 ,
,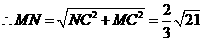 ,
, 中,
中,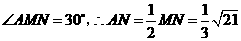 ,········································· 9分
,········································· 9分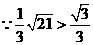 ,即
,即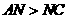 ,
, 直线
直线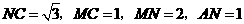 ,·············································· 11分
,·············································· 11分 ,
,

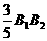 =0.6X,B1F=
=0.6X,B1F=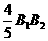 =0.8x
=0.8x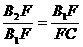 即
即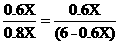
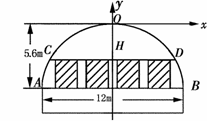
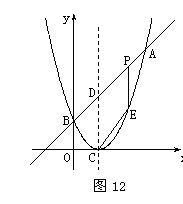 (08云南省卷24题) 24.(本大题满分14分)如图12,已知二次函数图象的顶点坐标为C(1,0),直线
(08云南省卷24题) 24.(本大题满分14分)如图12,已知二次函数图象的顶点坐标为C(1,0),直线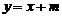 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴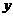 上.
上. 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;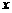 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为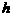 ,点P的横坐标为
,点P的横坐标为 得x2-3x+2=0.
………………………………(12分)
得x2-3x+2=0.
………………………………(12分)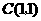 为圆心,2为半径作圆,交
为圆心,2为半径作圆,交 两点,开口向下的抛物线经过点
两点,开口向下的抛物线经过点 在
在 上.
上.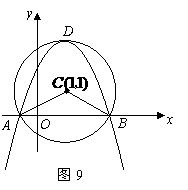 (1)求
(1)求 与
与 互相平分?若存在,求出点
互相平分?若存在,求出点 (08新疆乌鲁木齐23题解答)23.解:(1)作
(08新疆乌鲁木齐23题解答)23.解:(1)作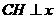 轴,
轴,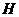 为垂足,
为垂足,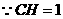 ,半径
,半径 ······················································ 1分
······················································ 1分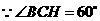 ,
,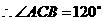 ······································ 3分
······································ 3分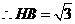 ,故
,故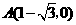 ,············································ 5分
,············································ 5分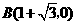 ········································································· 6分
········································································· 6分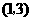 ··································· 7分
··································· 7分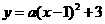 ·················································································· 8分
·················································································· 8分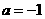 ······································································· 9分
······································································· 9分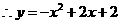 ····································································································· 10分
····································································································· 10分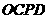 是平行四边形········· 11分
是平行四边形········· 11分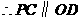 且
且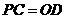 .
.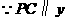 轴,
轴, 轴上.·············································································· 12分
轴上.·············································································· 12分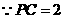 ,
,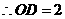 ,即
,即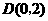 .
.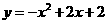 ,
, 解:(1)过
解:(1)过 作
作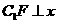 轴于点
轴于点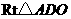 中,
中,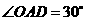 ,
,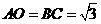
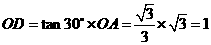 ································· 1分
································· 1分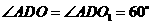
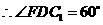
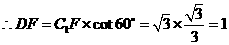 ············································································ 2分
············································································ 2分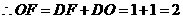
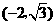 ····························································································· 3分
····························································································· 3分 的抛物线的解析式为
的抛物线的解析式为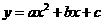 ,则
,则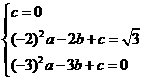 ································································································· 4分
································································································· 4分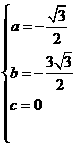
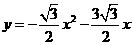 ································································· 5分
································································· 5分 与两坐标轴相切
与两坐标轴相切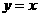 或
或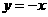 上·························································································· 6分
上·························································································· 6分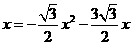
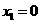 ,
,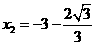
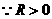
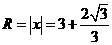 ····································································································· 7分
····································································································· 7分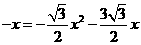
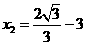
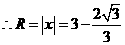
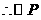 的半径
的半径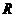 为
为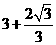 或
或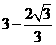 .······································································ 8分
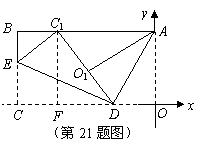
.······································································ 8分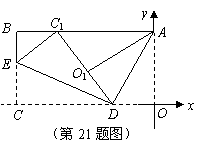 21.如图,已知平面直角坐标系中,有一矩形纸片
21.如图,已知平面直角坐标系中,有一矩形纸片 ,
, 为坐标原点,
为坐标原点,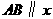 轴,
轴,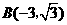 ,现将纸片按如图折叠,
,现将纸片按如图折叠,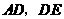 为折痕,
为折痕,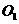 ,点
,点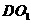 与
与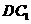 在同一直线上.
在同一直线上.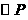 的半径为
的半径为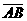 为圆O1、圆O2的公切线,
为圆O1、圆O2的公切线,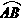 为半圆,且分别与三圆各切于一点。若圆O1、圆O2的半径均为1,则圆O3的半径为何?( )
为半圆,且分别与三圆各切于一点。若圆O1、圆O2的半径均为1,则圆O3的半径为何?( ) 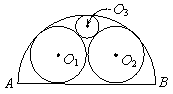

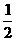 C.
C. 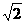 -1 D.
-1 D.