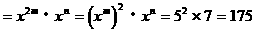0 47913 47921 47927 47931 47937 47939 47943 47949 47951 47957 47963 47967 47969 47973 47979 47981 47987 47991 47993 47997 47999 48003 48005 48007 48008 48009 48011 48012 48013 48015 48017 48021 48023 48027 48029 48033 48039 48041 48047 48051 48053 48057 48063 48069 48071 48077 48081 48083 48089 48093 48099 48107 447348
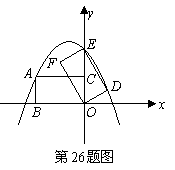
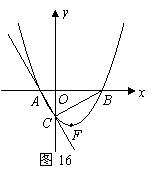 (08辽宁12市26题)(本题14分)26.如图16,在平面直角坐标系中,直线
(08辽宁12市26题)(本题14分)26.如图16,在平面直角坐标系中,直线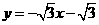 与
与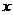 轴交于点
轴交于点 ,与
,与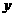 轴交于点
轴交于点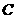 ,抛物线
,抛物线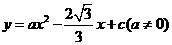 经过
经过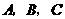 三点.
三点.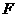 的坐标;
的坐标;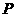 ,使
,使 为直角三角形,若存在,直接写出
为直角三角形,若存在,直接写出 上是否存在一点
上是否存在一点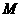 ,使得
,使得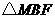 的周长最小,若存在,求出
的周长最小,若存在,求出 直线
直线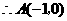 ,
,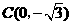 ························································································· 1分
························································································· 1分 都在抛物线上,
都在抛物线上,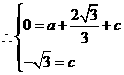
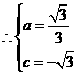
 抛物线的解析式为
抛物线的解析式为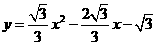 ························································ 3分
························································ 3分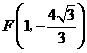 ······························································································· 4分
······························································································· 4分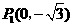 ············································································································· 7分
············································································································· 7分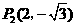 ············································································································ 9分
············································································································ 9分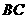 到点
到点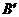 ,使
,使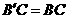 ,连接
,连接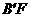 交直线
交直线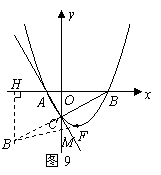 过点
过点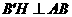 于点
于点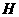 .
.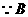 点在抛物线
点在抛物线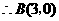
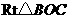 中,
中,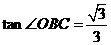 ,
,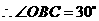 ,
,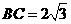 ,
,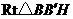 中,
中,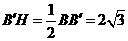 ,
,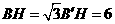 ,
,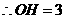 ,
,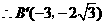 ··············································· 12分
··············································· 12分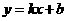
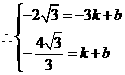 解得
解得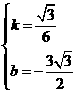
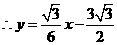 ································································································ 13分
································································································ 13分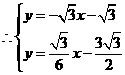 解得
解得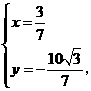
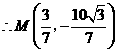
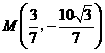 .··· 14分
.··· 14分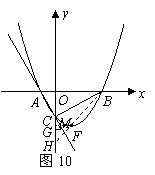 过点
过点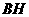 交
交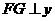 轴于点
轴于点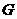 ,则
,则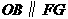 ,
,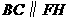 .
.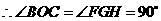 ,
,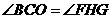
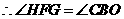
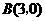 .
.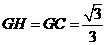 ,
, 为线段
为线段 的垂直平分线,可证得
的垂直平分线,可证得 为等边三角形,
为等边三角形, 垂直平分
垂直平分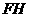 .
.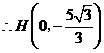 ············································· 12分
············································· 12分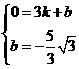 解得
解得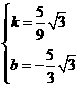
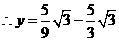 ································································································ 13分
································································································ 13分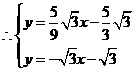 解得
解得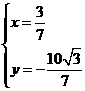
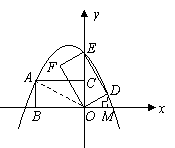
 (08辽宁沈阳26题)(本题14分)26.如图所示,在平面直角坐标系中,矩形
(08辽宁沈阳26题)(本题14分)26.如图所示,在平面直角坐标系中,矩形 的边
的边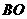 在
在 在
在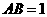 ,
,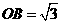 ,矩形
,矩形 按顺时针方向旋转
按顺时针方向旋转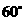 后得到矩形
后得到矩形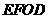 .点
.点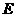 ,点
,点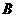 的对应点为点
的对应点为点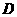 ,抛物线
,抛物线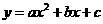 过点
过点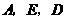 .
.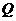 ,使以点
,使以点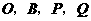 为顶点的平行四边形的面积是矩形
为顶点的平行四边形的面积是矩形 ,如图所示,在
,如图所示,在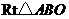 中,
中,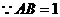 ,
,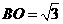 ,
,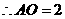
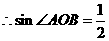 ,
,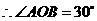
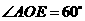
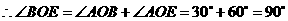
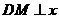 轴于点
轴于点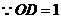 ,
,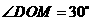
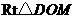 中,
中,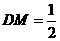 ,
,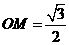
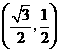 ·························································································· 5分
·························································································· 5分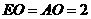 ,点
,点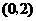
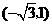 ···························································································· 6分
···························································································· 6分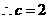
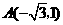 ,
,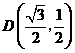 代入
代入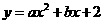 中得
中得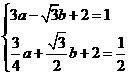 解得
解得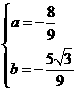
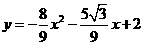 ······················································· 9分
······················································· 9分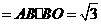
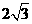 .
.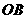 为此平行四边形一边,
为此平行四边形一边,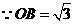
 边上的高为2··································································································· 11分
边上的高为2··································································································· 11分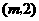
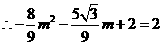
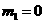 ,
,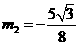
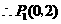 ,
,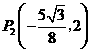
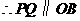 ,
,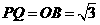 ,
,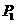 的坐标为
的坐标为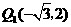 ,
,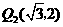 ;
;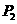 的坐标为
的坐标为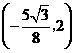 时,
时,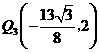 ,
,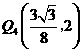 .··············································· 14分
.··············································· 14分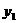 )、B(2a,y
)、B(2a,y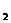 )、C(3a,y
)、C(3a,y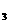 )都在抛物线
)都在抛物线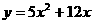 上.
上.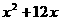 =0,·············································································· (1分)
=0,·············································································· (1分)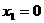 ,
,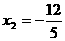 .·················································································· (2分)
.·················································································· (2分)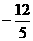 ,0).······································· (3分)
,0).······································· (3分) =S
=S -
- -
- ···················································· (5分)
···················································· (5分)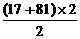 -
-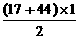 -
-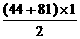 ···································· (6分)
···································· (6分)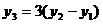 . ········································································· (8分)
. ········································································· (8分)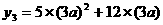 =45a2+36a.
=45a2+36a.
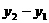 )=3[5×(2a)2+12×2a-(5a2+12a)] =45a2+36a.············ (9分)
)=3[5×(2a)2+12×2a-(5a2+12a)] =45a2+36a.············ (9分)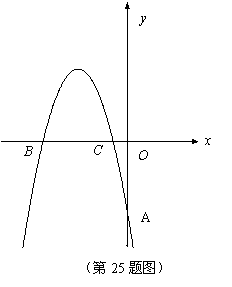 如图,在平面直角坐标系中,抛物线
如图,在平面直角坐标系中,抛物线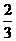
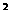 +
+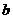
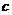 经过A(0,-4)、B(
经过A(0,-4)、B(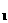 ,0)、 C(
,0)、 C(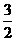
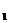 )
)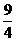
 ··········································································································· 3分
··········································································································· 3分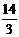 . ·········································································································· 4分
. ·········································································································· 4分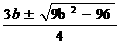 ,··········································································· 2分
,··········································································· 2分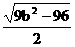 =5,
=5,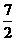 )
)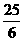 ································· 6分
································· 6分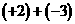 ,不能写成“
,不能写成“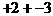 ”。其次,要牢记运算的法则。第三,减法统一变加法。因为学了相反数后,减去一个数,等于加上这个数的相反数。这是有理数的减法法则,它把减法变成了加法。
”。其次,要牢记运算的法则。第三,减法统一变加法。因为学了相反数后,减去一个数,等于加上这个数的相反数。这是有理数的减法法则,它把减法变成了加法。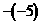 ,表示
,表示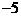 的相反数。
的相反数。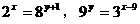 ,试求
,试求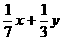 的值。
的值。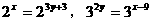
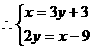
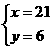
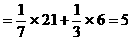
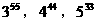 的大小。
的大小。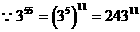
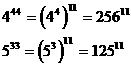
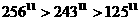
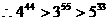
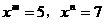 ,求
,求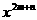 的值。
的值。