0 47921 47929 47935 47939 47945 47947 47951 47957 47959 47965 47971 47975 47977 47981 47987 47989 47995 47999 48001 48005 48007 48011 48013 48015 48016 48017 48019 48020 48021 48023 48025 48029 48031 48035 48037 48041 48047 48049 48055 48059 48061 48065 48071 48077 48079 48085 48089 48091 48097 48101 48107 48115 447348
 中
中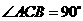 ,
,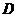 是
是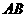 的中点,以
的中点,以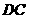 为直径的
为直径的 交
交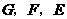 点.
点.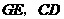 的交点为
的交点为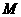 ,且
,且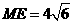 ,
, .
.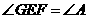 .
.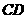 的长.
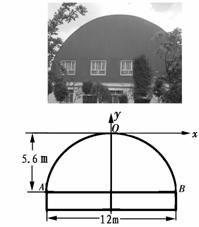
的长.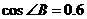 ,以
,以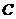 为坐标原点,
为坐标原点,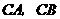 所在的直线分别为
所在的直线分别为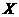 轴和
轴和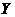 轴,建立平面直角坐标系,求直线
轴,建立平面直角坐标系,求直线
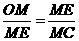 ∴
∴ 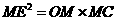
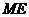 =
=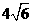 ∴
∴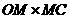 =
=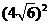 =96
=96
 MC=8
MC=8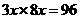 ∴
∴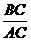 ∴BC=24 ∴ AC=32
∴BC=24 ∴ AC=32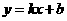 根据题意得 A (32,0) B(0,24)
根据题意得 A (32,0) B(0,24)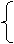
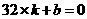
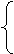
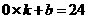 解得
解得 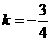
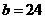 ∴
∴
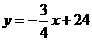
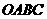 中,
中, ,
, 为坐标原点,点
为坐标原点,点 在
在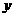 轴正半轴上,点
轴正半轴上,点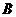 坐标为(2,2
坐标为(2,2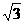 ),∠
),∠ = 60°,
= 60°,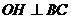 于点
于点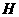 .动点
.动点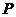 从点
从点 向点
向点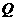 从点
从点 向点
向点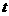 秒.
秒. 的长;
的长;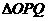 的面积为
的面积为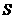 (平方单位). 求
(平方单位). 求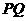 与
与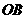 交于点
交于点 为等腰三角形时,求(2)中
为等腰三角形时,求(2)中 长度的最大值是多少,直接写出结论.
长度的最大值是多少,直接写出结论.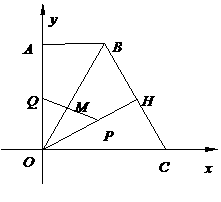
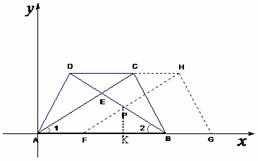
 中,
中,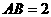 ,
,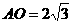
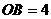 ,
, 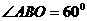
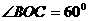 而
而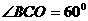
 为等边三角形
为等边三角形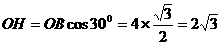 …(3分)
…(3分)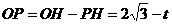
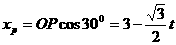
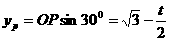
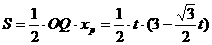
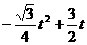 (
(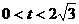 )…………………………(6分)
)…………………………(6分)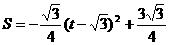
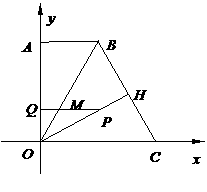 ∴当
∴当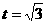 时,
时,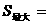
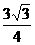 ………………………………………(7分)
………………………………………(7分)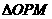 为等腰三角形,则:
为等腰三角形,则: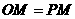 ,
,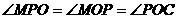
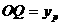 即
即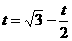
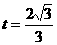
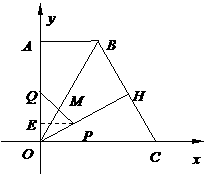 此时
此时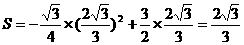 ………………………………(8分)
………………………………(8分)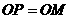 ,
,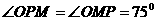
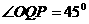
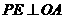 ,垂足为
,垂足为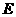 ,则有:
,则有: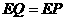
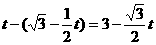
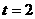
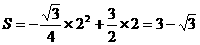 ……………………………………(9分)
……………………………………(9分)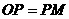 ,
,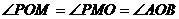
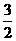 ……………………………………………………(12分)
……………………………………………………(12分)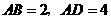 ,
,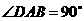 ,
,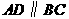 (如图).
(如图).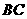 上的动点(点
上的动点(点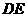 的中点.
的中点.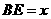 ,
,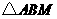 的面积为
的面积为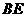 的长;
的长;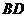 ,交线段
,交线段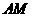 于点
于点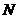 ,如果以
,如果以 为顶点的三角形与
为顶点的三角形与 相似,求线段
相似,求线段

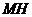 ,
,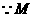 为
为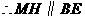 ,
,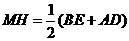 .
.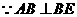 ,
,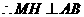 .
.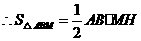 ,得
,得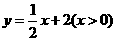 ;
;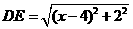 .
. 以线段
以线段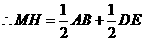 ,即
,即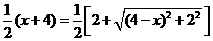 .
.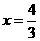 ,即线段
,即线段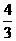 ;
;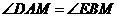 .
.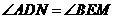 ;②
;②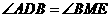 .
.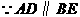 ,
,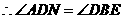 .
.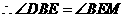 .
.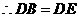 ,易得
,易得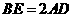 .得
.得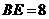 ;
;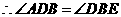 .
.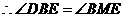 .又
.又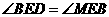 ,
,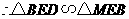 .
.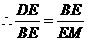 ,即
,即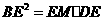 ,得
,得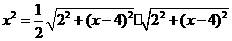 .
.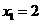 ,
,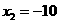 (舍去).即线段
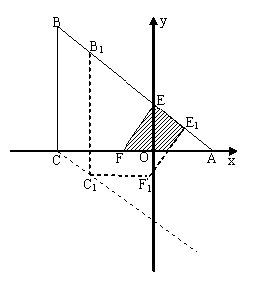
(舍去).即线段 (2008湖北荆州)如图,等腰直角三角形纸片ABC中,AC=BC=4,∠ACB=90º,直角边AC在x轴上,B点在第二象限,A(1,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在直线重合,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA平移,至B点到达A点停止.设平移时间为t(s),移动速度为每秒1个单位长度,平移中四边形BCFE与△AEF重叠的面积为S.
(2008湖北荆州)如图,等腰直角三角形纸片ABC中,AC=BC=4,∠ACB=90º,直角边AC在x轴上,B点在第二象限,A(1,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在直线重合,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA平移,至B点到达A点停止.设平移时间为t(s),移动速度为每秒1个单位长度,平移中四边形BCFE与△AEF重叠的面积为S.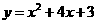 的顶点?若存在,求出t值;若不存在,请说明理由;
的顶点?若存在,求出t值;若不存在,请说明理由;

 ∥BA 交Y轴于P,
∥BA 交Y轴于P,

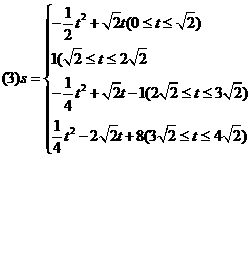
 ,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由。
,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由。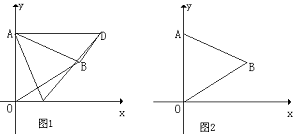
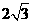 ,
,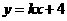 ,所以
,所以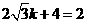 ,解得
,解得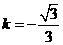 ,的以直线AB的解析式为
,的以直线AB的解析式为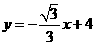
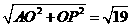
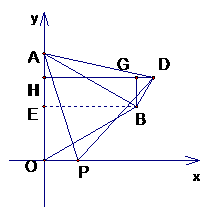
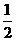 BD=
BD=
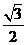 ,DH=GH+GD=
,DH=GH+GD=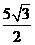 ,
,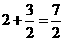
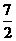 )
)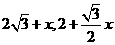 )
)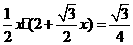
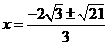
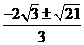 ,0)
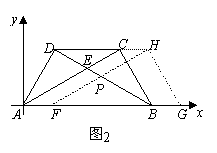
,0) 中,点
中,点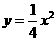 在第一象限内的图象上的任一点,点
在第一象限内的图象上的任一点,点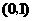 ,直线
,直线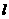 过
过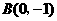 且与
且与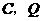 ,连结
,连结 交
交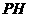 交
交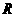 .
.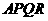 为平行四边形;
为平行四边形;

 .
. ,
, ,
,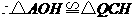 .
.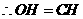 ,即
,即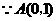 ,
,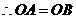 .
.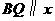 轴,
轴,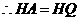 .
.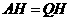 ,
,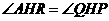 ,
,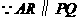 ,
,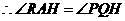 ,
,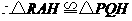 .
.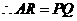 ,
,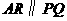 ,
, 四边形
四边形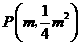 ,
,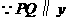 轴,则
轴,则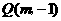 ,则
,则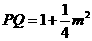 .
.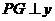 轴,垂足为
轴,垂足为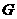 ,在
,在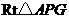 中,
中,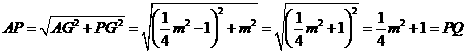 .
.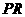 为
为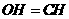 ,得
,得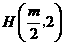 ,
,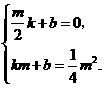
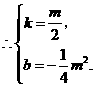
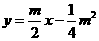 .
.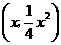 ,代入直线
,代入直线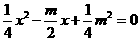 ,
,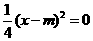 ,解得
,解得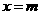 .得公共点为
.得公共点为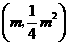 .
.
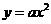
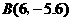 在抛物线的图象上.
在抛物线的图象上.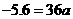
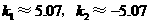 (舍去)
(舍去)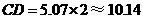 (m)
(m)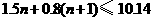
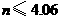 .
.

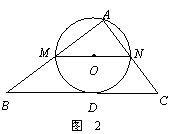


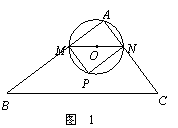 ∴ △AMN ∽ △ABC.
∴ △AMN ∽ △ABC.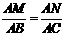 ,即
,即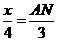 .
.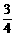 x.
x. 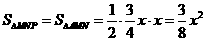 .(0<
.(0<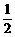 MN.
MN.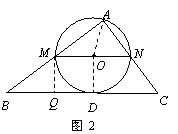
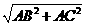 =5.
=5.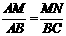 ,即
,即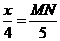 .
. 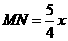 ,
,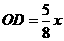 .
.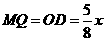 .
. 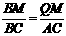 .
.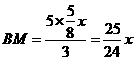 ,
,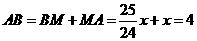 .
. 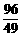 .
. 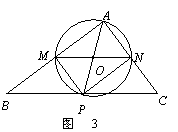 (3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.
(3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.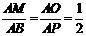 . AM=MB=2.
. AM=MB=2.
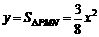 .
. 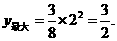
 ∵ 四边形AMPN是矩形,
∵ 四边形AMPN是矩形,
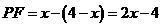 .
. 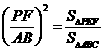 .
.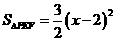 .
. 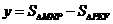 =
=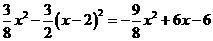 .
.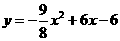
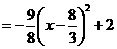 .
. 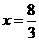 时,满足2<
时,满足2<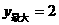 .
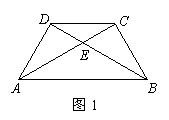
.


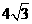 ,
,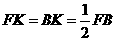 .
.
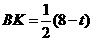 .
.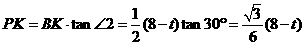 .
. 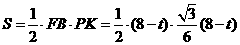 ,
,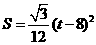 ,或
,或 .
.  .
.