摘要:已知向量和.且求的值. 袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为现有甲.乙两人从袋中轮流摸取1球.甲先取.乙后取.然后甲再取--取后不放回.直到两人中有一人取到白球时既终止.每个球在每一次被取出的机会是等可能的.用表示取球终止所需要的取球次数. (I)求袋中原有白球的个数, (II)求随机变量的概率分布, (III)求甲取到白球的概率. 已知是函数的一个极值点.其中. (I)求与的关系式, (II)求的单调区间, (III)当时.函数的图象上任意一点的切线斜率恒大于3.求的取值范围. 如图.已知长方体直线与平面所成的角为.垂直于.为的中点. (I)求异面直线与所成的角, (II)求平面与平面所成的二面角, (III)求点到平面的距离. 已知数列的首项前项和为.且 (I)证明数列是等比数列, (II)令.求函数在点处的导数并比较与的大小. 已知动圆过定点.且与直线相切.其中. (I)求动圆圆心的轨迹的方程, (II)设A.B是轨迹上异于原点的两个不同点.直线和的倾斜角分别为和.当变化且为定值时.证明直线恒过定点.并求出该定点的坐标.
网址:http://m.1010jiajiao.com/timu3_id_4469228[举报]
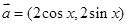 ,
, ,函数
,函数 .
. 的最小正周期和值域;
的最小正周期和值域;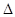
 中,
中,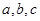 分别是角
分别是角 的对边,且
的对边,且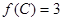 ,
, ,
, ,且
,且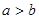 ,求
,求
