0 446754 446762 446768 446772 446778 446780 446784 446790 446792 446798 446804 446808 446810 446814 446820 446822 446828 446832 446834 446838 446840 446844 446846 446848 446849 446850 446852 446853 446854 446856 446858 446862 446864 446868 446870 446874 446880 446882 446888 446892 446894 446898 446904 446910 446912 446918 446922 446924 446930 446934 446940 446948 447348
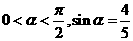
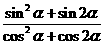 的值;
的值;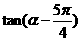 的值。
的值。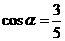 ,所以
,所以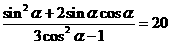 。
。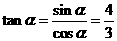 ,∴
,∴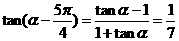 。
。 (Ⅰ)芳香度之和等于4的取法有2种:
(Ⅰ)芳香度之和等于4的取法有2种: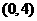 、
、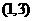 ,故
,故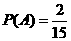 。
。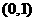 ;芳香度之和等于2的取法有1种:
;芳香度之和等于2的取法有1种: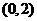 ,故
,故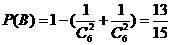 。
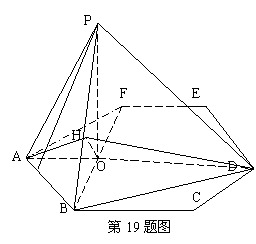
。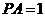 ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。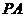 ⊥
⊥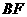 ;
;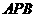 与面
与面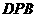 所成二面角的大小。
所成二面角的大小。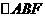 为等腰三角形,
为等腰三角形,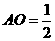 ,
,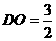 ,
,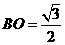 。
。 为所求二面角平面角。
为所求二面角平面角。 中,OH=
中,OH=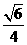 ,
,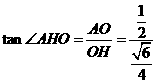 =
=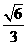 。
。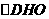 中,
中,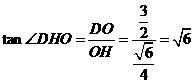 ;
;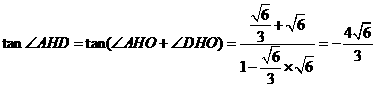
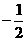 ,0),B(
,0),B(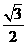 ,0,0),D(0,2,0),∴
,0,0),D(0,2,0),∴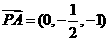 ,
,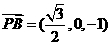 ,
,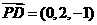
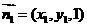 ,则
,则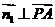 ,
,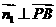 ,得
,得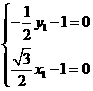 ,
,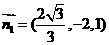 ;
;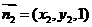 ,则
,则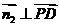 ,
,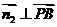 ,得
,得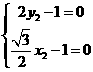 ,
,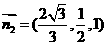 ;
;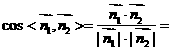
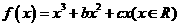 ,已知
,已知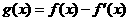 是奇函数。
是奇函数。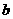 、
、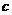 的值。
的值。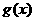 的单调区间与极值。
的单调区间与极值。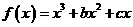 ,∴
,∴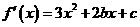 。从而
。从而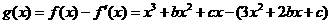 =
=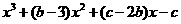 是一个奇函数,所以
是一个奇函数,所以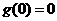 得
得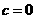 ,由奇函数定义得
,由奇函数定义得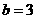 ;
;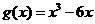 ,从而
,从而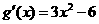 ,由此可知,
,由此可知,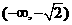 和
和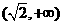 是函数
是函数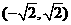 是函数
是函数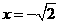 时,取得极大值,极大值为
时,取得极大值,极大值为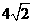 ,
,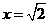 时,取得极小值,极小值为
时,取得极小值,极小值为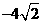 。
。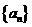 中,
中,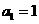 ,前
,前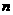 项和
项和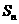 满足条件
满足条件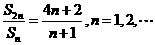 ,
, 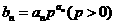 ,求数列
,求数列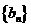 的前
的前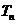 。
。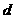 ,由
,由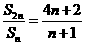 得:
得: ,所以
,所以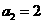 ,即
,即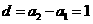 ,又
,又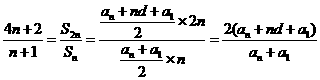 =
=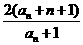 ,所以
,所以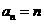 。
。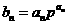 ,得
,得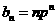 。所以
。所以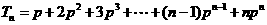 ,
,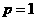 时,
时,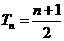 ;
;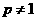 时,
时, ,
,
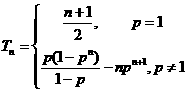 。
。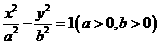 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于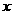 轴上方,M为左准线上一点,
轴上方,M为左准线上一点, 为坐标原点。已知四边形
为坐标原点。已知四边形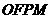 为平行四边形,
为平行四边形,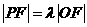 。
。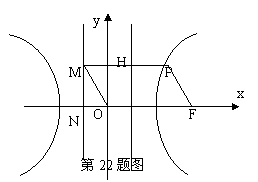 (Ⅰ)写出双曲线C的离心率
(Ⅰ)写出双曲线C的离心率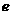 与
与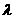 的关系式;
的关系式;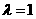 时,经过焦点F且平行于OP的直线交双曲线于A、B点,若
时,经过焦点F且平行于OP的直线交双曲线于A、B点,若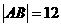 ,求此时的双曲线方程。
,求此时的双曲线方程。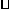 ,∴
,∴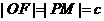 ,作双曲线的右准线交PM于H,则
,作双曲线的右准线交PM于H,则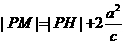 ,又
,又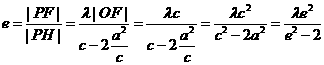 ,
,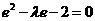 。
。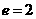 ,
,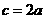 ,
,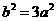 ,双曲线为
,双曲线为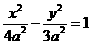 ,设P
,设P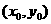 ,则
,则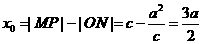 ,
,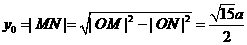 ,所以直线OP的斜率为
,所以直线OP的斜率为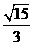 ,则直线AB的方程为
,则直线AB的方程为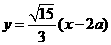 ,代入到双曲线方程得:
,代入到双曲线方程得: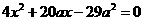 ,
,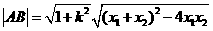 得:
得: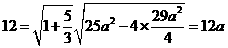 ,解得
,解得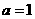 ,则
,则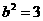 ,所以
,所以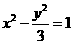 为所求。
为所求。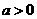 ,
,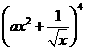 展开式中
展开式中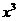 的系数为
的系数为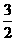 ,则
,则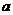 =_____。
=_____。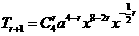 ,由
,由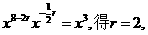
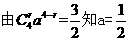 。
。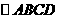 中,
中,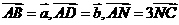 ,M为BC的中点,则
,M为BC的中点,则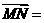 _______。(用
_______。(用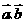 表示)
表示)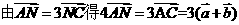 ,
,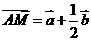 ,所以
,所以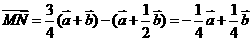 。
。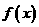 对于任意实数
对于任意实数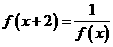 ,若
,若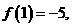 则
则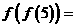 __________。
__________。 ,所以
,所以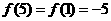 ,则
,则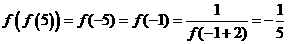 。
。 内,其余顶点在
内,其余顶点在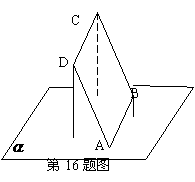 解:如图,B、D到平面
解:如图,B、D到平面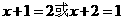 ,即
,即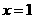 ,所以D到平面
,所以D到平面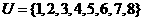 ,集合
,集合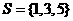 ,
,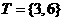 ,则
,则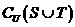 等于( )
等于( )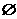 B.
B.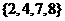 C.
C.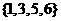 D.
D.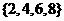
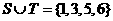 ,则
,则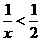 的解集是( )
的解集是( )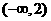 B.
B.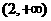 C.
C.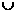
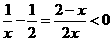 ,即
,即 ,故选D。
,故选D。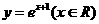 的反函数是( )
的反函数是( ) B.
B.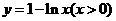
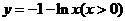 D.
D.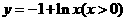
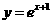 得:
得: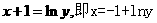 ,所以
,所以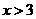 ”是
”是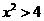 “的( )
“的( )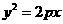 的焦点与椭圆
的焦点与椭圆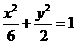 的右焦点重合,则
的右焦点重合,则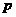 的值为( )
的值为( )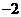 B.
B.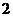 C.
C.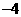 D.
D.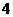
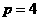 ,故选D。
,故选D。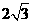 的正八面体的各个顶点都在同一个球面上,则此球的体积为
的正八面体的各个顶点都在同一个球面上,则此球的体积为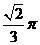 B.
B.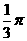 C.
C.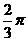 D.
D.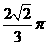
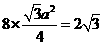 知,
知,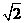 ,故选A。
,故选A。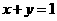 与圆
与圆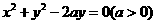 没有公共点,则
没有公共点,则 B.
B.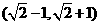 C.
C.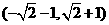 D.
D.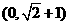
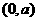 到直线
到直线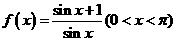 ,下列结论正确的是( )
,下列结论正确的是( )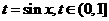 ,则函数
,则函数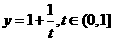 的值域,而
的值域,而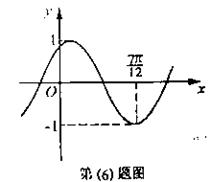 (9)将函数
(9)将函数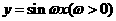 的图象按向量
的图象按向量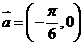 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )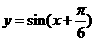 B.
B.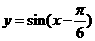
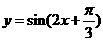 D.
D.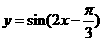
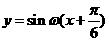 ,由图象知,
,由图象知,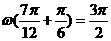 ,所以
,所以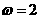 ,因此选C。
,因此选C。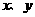 满足条件
满足条件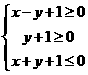 ,那么
,那么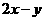 的最大值为( )
的最大值为( )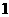 C.
C.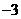
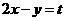 过点(0,-1)时,
过点(0,-1)时,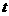 最大,故选B。
最大,故选B。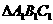 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于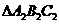 的三个内角的正弦值,则( )
的三个内角的正弦值,则( )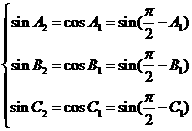 ,得
,得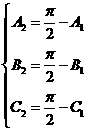 ,那么,
,那么,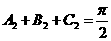 ,所以
,所以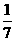 B.
B.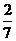 C.
C.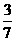 D.
D.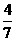
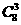 个三角形,要得直角非等腰三角形,则每个顶点上可得三个(即正方体的一边与过此点的一条面对角线),共有24个,得
个三角形,要得直角非等腰三角形,则每个顶点上可得三个(即正方体的一边与过此点的一条面对角线),共有24个,得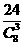 ,所以选C。
,所以选C。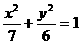 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为
.
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为
.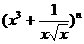 的展开式中的常数项为84,则n=
.
的展开式中的常数项为84,则n=
.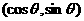 ,向量b=
,向量b=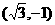 ,则|2a-b|的最大值是
.
,则|2a-b|的最大值是
.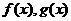 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当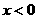 时,
时,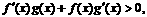
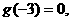 则不等式
则不等式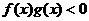 的解集是________________________.
的解集是________________________. 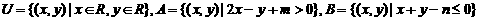 ,那么点P(2,3)
,那么点P(2,3) (
(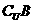 )的充要条件是 ( )
)的充要条件是 ( )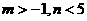 B.
B.
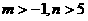 D.
D.