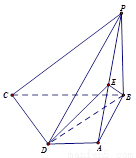
摘要:20. 如图.直二面角D-AB-E中.四边形ABCD是边长为2的正方形.AE=EB.F为CE上的点.且BF⊥平面ACE. (Ⅰ)求证AE⊥平面BCE, (Ⅱ)求二面角B-AC-E的大小, (Ⅲ)求点D到平面ACE的距离. 解法一:(Ⅰ) ∵BF⊥平面ACE,∴BF⊥AE,∵二面角D-AB-E为直二面角,且CB⊥AB, ∴CB⊥平面ABE,∴CB⊥AE,∴AE⊥平面BCE (Ⅱ)连结BD交AC于G,连结FG,∵正方形ABCD边长为2,∴BG⊥AC,BG=, ∵BF⊥平面ACE,由三垂线定理的逆定理得FG⊥AC,∴∠BCF是二面角B-AC-E的平面角, 由(Ⅰ)AE⊥平面BCE,∴AE⊥EB.又∵AE=EB,∴在等腰直角三角形中,BE=. 又∵直角三角形BCE中,EC=,BF= ∴直角三角形BFG中,sin∠BGF=,∴二面角B-AC-E等于arcsin. ,(Ⅲ)过E作EO⊥AB交AB于O,OE=1,∵二面角D-AB-E为直二面角,∴EO⊥平面ABCD. 设D到平面ACE的距离为h,∵,∴. ∵AE⊥平面BCE,∴AE⊥EC.∴h=. ∴点D点D到平面ACE的距离为. 解法二:(Ⅰ)同解法一. (Ⅱ)以线段AB的中点为原点O,OE所在直线为x轴,AB所在直线为y轴,过O点平行于AD的直线为z轴,建立空间直角坐标系O-xyz,如图 ∵AE⊥平面BCE,BE面BCE,∴AE⊥BE,在直角三角形AEB中,AB=2,O为AB的中点 ∴OE=1,A,C, 设平面AEC的一个法向量=,则即解得 令x=1,得=是平面EAC的一个法向量,又平面BAC的一个法向量为=, ∴cos()= ∴二面角B-AC-E的大小为arccos. (Ⅲ)∵AD∥z轴,AD=2,∴,∴点D到平面ACE的距离 d=||.
网址:http://m.1010jiajiao.com/timu3_id_4469067[举报]
1. (本小题满分12分)
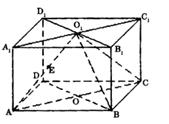
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB = 60°的菱形,AC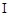 BD = O,A1C1
BD = O,A1C1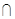 B1D1
= O1,E是O1A的中点.
B1D1
= O1,E是O1A的中点.
(1) 求二面角O1-BC-D的大小;
(2) 求点E到平面O1BC的距离.
|
查看习题详情和答案>>
19. (本小题满分12分)
如图,直四棱柱ABCD—A1B1C1D1的高为3,底面是边长为4且∠DAB = 60°的菱形,AC
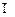 BD = O,A1C1
BD = O,A1C1 B1D1 = O1,E是O1A的中点.
B1D1 = O1,E是O1A的中点.(1) 求二面角O1-BC-D的大小;
(2) 求点E到平面O1BC的距离.
|
(本小题满分12分)如图,在直三棱柱ABC―A1B1C1中,∠ACB = 90°. AC = BC = a,
D、E分别为棱AB、BC的中点, M为棱AA1上的点,二面角M―DE―A为30°.
(1)求MA的长;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)求点C到平面MDE的距离。


 .
. 平面B1C1D;
平面B1C1D;
 底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.