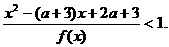19.(12分)已知数列{an}的前n项和Sn满足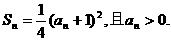
(1)求a1,a2及{an}的通项公式;
(2)令bn=20-an,问数列{bn}的前多少项的和最大?
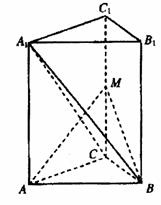 20.(12分)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA=
20.(12分)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA= ,AA1=
,AA1=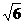 M为侧棱CC1上一点,AM⊥A1C;
M为侧棱CC1上一点,AM⊥A1C;
(1)求证:B1C1//平面A1BC;
(2)求异面直线A1B与AC所成的
角的余弦值;
(3)求点C到平面ABM的距离.
 21.(12分)如图,ABCD是一块边长为4km的正方形地域,地域内有一条河流MD,河流经过路线是以AB中点M为顶点且开口向右的抛物线(河流宽度忽略不计),某公司准备投巨资建一个大型矩形游乐园PQCN(如图),问如何施工才能使游乐园面积最大,并求出最大值.
21.(12分)如图,ABCD是一块边长为4km的正方形地域,地域内有一条河流MD,河流经过路线是以AB中点M为顶点且开口向右的抛物线(河流宽度忽略不计),某公司准备投巨资建一个大型矩形游乐园PQCN(如图),问如何施工才能使游乐园面积最大,并求出最大值.
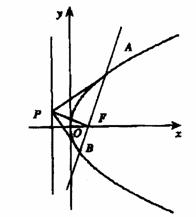 22.(12分)如图,设抛物线
22.(12分)如图,设抛物线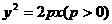 的焦点为F,经过点F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1),(x2,y2),y1>0,y2<0,P是此抛物线的准线上的一点,0是坐标原点.
的焦点为F,经过点F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1),(x2,y2),y1>0,y2<0,P是此抛物线的准线上的一点,0是坐标原点.
|
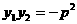
(2)若直线PA、PF、PB的方向向量分
别为(1,a)、(1,b)、(1,c),
求证:实数a、b、c成等差数列;
(3)若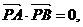 ∠APF=
∠APF=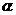 ,∠BPF=
,∠BPF=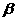 ,
,
∠PFO=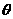 ,求证:
,求证: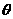 =|
=|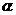 -
-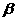 |.
|.
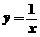 的图象是双曲线,则它的一个焦点坐标是
的图象是双曲线,则它的一个焦点坐标是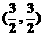 (B)
(B)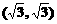
 (C)
(C)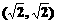 (D)
(D)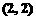
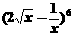 展开式的第5项等于
展开式的第5项等于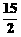 ,则x的值是
,则x的值是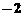 (C)
(C) (D)
(D)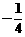
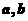 ,平面
,平面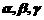 ,则使
,则使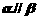 成立的一个充分条件是
成立的一个充分条件是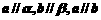 (B)
(B)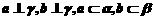
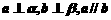 (D)
(D)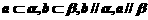
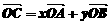 ,则
,则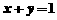 (B)
(B)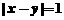
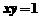 (D)
(D)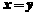
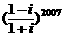 的值是
的值是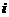 (C)
(C)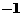 (D)
(D)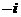
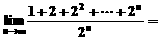
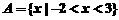 ,
,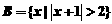 ,则
,则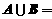
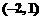 (B)
(B)
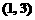 (D)
(D)