|
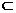 {1,2,3},且A的元素中至少含有一个奇数,则满足条件的集合A共有
{1,2,3},且A的元素中至少含有一个奇数,则满足条件的集合A共有
( )
A.6个 B.5个 C.4个 D.3个
2.若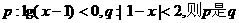 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
|
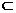 {1,2,3},且A的元素中至少含有一个奇数,则满足条件的集合A共有
{1,2,3},且A的元素中至少含有一个奇数,则满足条件的集合A共有
( )
A.6个 B.5个 C.4个 D.3个
2.若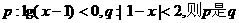 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件