0 137949 137957 137963 137967 137973 137975 137979 137985 137987 137993 137999 138003 138005 138009 138015 138017 138023 138027 138029 138033 138035 138039 138041 138043 138044 138045 138047 138048 138049 138051 138053 138057 138059 138063 138065 138069 138075 138077 138083 138087 138089 138093 138099 138105 138107 138113 138117 138119 138125 138129 138135 138143 447348
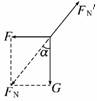 D.FN=
D.FN=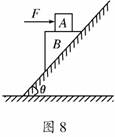 答案:AD
答案:AD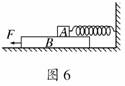 如图6所示,一木板B放在粗糙的水平地面上,木块A放在B的上面,A的右端通过轻质水平弹簧与竖直墙壁连接.现用水平力F向左拉B,使B以速度v向左匀速运动,这时弹簧对木块A的拉力大小为FT.则下列说法正确的是
( )
如图6所示,一木板B放在粗糙的水平地面上,木块A放在B的上面,A的右端通过轻质水平弹簧与竖直墙壁连接.现用水平力F向左拉B,使B以速度v向左匀速运动,这时弹簧对木块A的拉力大小为FT.则下列说法正确的是
( )  答案:BD
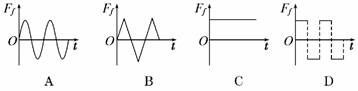
答案:BD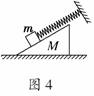 如图4所示,斜面体M的底面粗糙,斜面光滑,放在粗糙水平面上.弹簧的一端固定在墙面上,另一端与放在斜面上的物块m相连,弹簧的轴线与斜面平行.若物块在斜面上做简谐运动,斜面体保持静止,则地面对斜面体的摩擦力Ff与时间t的关系图象是图5中的
( )
如图4所示,斜面体M的底面粗糙,斜面光滑,放在粗糙水平面上.弹簧的一端固定在墙面上,另一端与放在斜面上的物块m相连,弹簧的轴线与斜面平行.若物块在斜面上做简谐运动,斜面体保持静止,则地面对斜面体的摩擦力Ff与时间t的关系图象是图5中的
( )
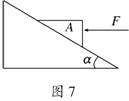
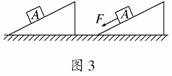 (2010·合肥模拟)如图3所示,斜面固定在水平地面上,先让物体A沿斜面下滑,恰能匀速.后给A一个沿斜面向下的力F,让其加速下滑.设前后两次A与斜面间的摩擦力分别为Ff1、Ff2,地面对斜面的支持力分别为FN1、FN2,则 ( )
(2010·合肥模拟)如图3所示,斜面固定在水平地面上,先让物体A沿斜面下滑,恰能匀速.后给A一个沿斜面向下的力F,让其加速下滑.设前后两次A与斜面间的摩擦力分别为Ff1、Ff2,地面对斜面的支持力分别为FN1、FN2,则 ( ) 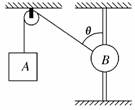
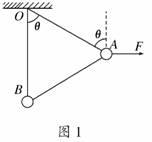 (2010·福州模拟)两个相同的可视为质点的小球A和B,质量均为m,用长度相同的两根细线把A、B两球悬挂在水平天花板上的同一点O,并用长度相同的细线连接A、B两个小球,然后用一水平方向的力F作用在小球A上,此时三根线均处于伸直状态,且OB细线恰好处于竖直方向,如图1所示.如果两小球均处于静止状态,则力F的大小为( )
(2010·福州模拟)两个相同的可视为质点的小球A和B,质量均为m,用长度相同的两根细线把A、B两球悬挂在水平天花板上的同一点O,并用长度相同的细线连接A、B两个小球,然后用一水平方向的力F作用在小球A上,此时三根线均处于伸直状态,且OB细线恰好处于竖直方向,如图1所示.如果两小球均处于静止状态,则力F的大小为( ) 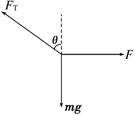
 ①还缺少的器材有_______________________________________________________;
①还缺少的器材有_______________________________________________________; 在水面上;
在水面上;