2009年江苏省高考数学重点内容分类精析
一.集合(集合及其表示A;子集B,交集、并集、补集B)
1.
满足 ,且
,且
 的集合
的集合 的个数是 2
的个数是 2
2.
设 是一个数集,且至少含有两个数,若对任意
是一个数集,且至少含有两个数,若对任意 都有
都有 (除数
(除数 ),则称P是一个数域,例如有理数Q是数域。有下列命题:①数域必含有0,1两个数;②整数集是数域;③若有理数
),则称P是一个数域,例如有理数Q是数域。有下列命题:①数域必含有0,1两个数;②整数集是数域;③若有理数 ,则数集
,则数集 必为数域;④数域必为无限集。
必为数域;④数域必为无限集。
其正确的命题的序号是 ①④ (把你认为正确的命题的序号都填上)
二.函数概念与基本初等函数Ⅰ(函数的概念B;函数的基本性质B)
3.
若函数 的定义域是
的定义域是 ,则函数
,则函数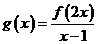 的定义域是 [0,1]
的定义域是 [0,1]
4.
定义在R上的函数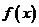 满足
满足 ,
, ,则
,则 等于
等于
6
5.
设函数 ,则
,则 的值为
的值为
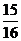
三.函数概念与基本初等函数Ⅰ(指数与对数B;指数与对数的图象和性质B;对数函数的图象和性质B;幂函数A;函数与方程A;函数模型及其应用B))
6.则下列四个结论正确的是 ③ (填正确序号)
①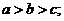 ②
②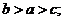 ③
③ ; ④
; ④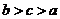
7.已知函数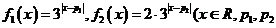 为常当选),函数
为常当选),函数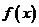 的定义为:对每一个给定的实数
的定义为:对每一个给定的实数 ,
,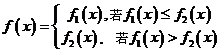
(1)
求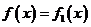 对所有实数
对所有实数 成立的充分必要条件(用
成立的充分必要条件(用 表示)
表示)
(2)
设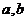 是两个实数,满足
是两个实数,满足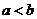 且
且 ,若
,若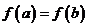 ,求证:函数
,求证:函数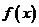 在区间
在区间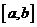 上的单调增区间的长度之和为
上的单调增区间的长度之和为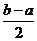 (闭区间
(闭区间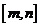 的长度定义为
的长度定义为 )
)
解:(1)由 的定义可知,
的定义可知, (对所有实数
(对所有实数 )等价于
)等价于
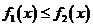 (对所有实数
(对所有实数 )这又等价于
)这又等价于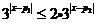 ,即
,即
 对所有实数
对所有实数 均成立. (*)
均成立. (*)
由于 的最大值为
的最大值为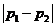 ,
,
故(*)等价于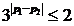 ,即
,即 ,这就是所求的充分必要条件
,这就是所求的充分必要条件
(2)分两种情形讨论
(i)当 时,由(1)知
时,由(1)知 (对所有实数
(对所有实数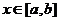 )
)
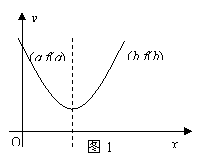 则由
则由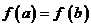 及
及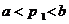 易知
易知 ,
,
再由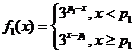 的单调性可知,
的单调性可知,
函数 在区间
在区间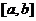 上的单调增区间的长度
上的单调增区间的长度
为 (参见示意图1)
(参见示意图1)
(ii)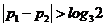 时,不妨设
时,不妨设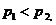 ,则
,则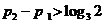 ,于是
,于是
当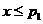 时,有
时,有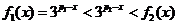 ,从而
,从而 ;
;
当 时,有
时,有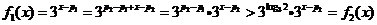
从而  ;
;
当 时,
时,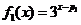 ,及
,及 ,由方程
,由方程
 解得
解得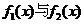 图象交点的横坐标为
图象交点的横坐标为
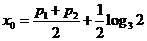 ⑴
⑴
显然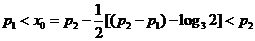 ,
,
这表明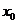 在
在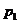 与
与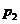 之间。由⑴易知
之间。由⑴易知

综上可知,在区间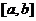 上,
上,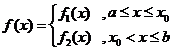 (参见示意图2)
(参见示意图2)
故由函数 及
及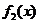 的单调性可知,
的单调性可知, 在区间
在区间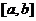 上的单调增区间的长度之和为
上的单调增区间的长度之和为 ,由于
,由于 ,即
,即 ,得
,得
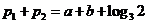 ⑵
⑵
故由⑴、⑵得 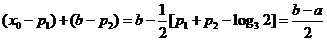
综合(i)(ii)可知, 在区间
在区间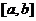 上的单调增区间的长度和为
上的单调增区间的长度和为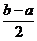 。
。
8.
已知二次函数
(1)
若函数在区间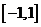 上存在零点,求实数
上存在零点,求实数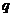 的取值范围;
的取值范围;
(2)
问:是否存在常数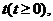 当
当 时,
时,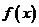 的值域为区间D,且D的长度为
的值域为区间D,且D的长度为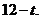
9.水库的蓄水量随时间而变化,现用 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于 的近似函数关系式为
的近似函数关系式为

(Ⅰ)该水库的蓄求量小于50的时期称为枯水期.以 表示第1月份(
表示第1月份(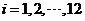 ),问一年内哪几个月份是枯水期?
),问一年内哪几个月份是枯水期?
(Ⅱ)求一年内该水库的最大蓄水量(取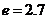 计算).
计算).
解:本小题主要考查函数、导数和不等式等基本知识,考查用导数求最值和综合运用数学知识解决实际问题能力.
(Ⅰ)①当 时,
时, ,化简得
,化简得 ,
,
解得 ,或
,或 ,又
,又 ,故
,故 .
.
②当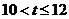 时,
时,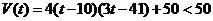 ,化简得
,化简得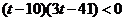 ,
,
解得 ,又
,又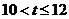 ,故
,故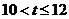 .
.
综合得 ,或
,或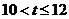 ;
;
故知枯水期为1月,2月,3月,11月,12月共5个月.
(Ⅱ)(Ⅰ)知:V(t)的最大值只能在(4,10)内达到.
由V′(t)=

令V′(t)=0,解得t=8(t=-2舍去).
当t变化时,V′(t) 与V (t)的变化情况如下表:
t
(4,8)
8
(8,10)
V′(t)
+
0
-
V(t)

极大值

由上表,V(t)在t=8时取得最大值V(8)=8e2+50-108.52(亿立方米).
故知一年内该水库的最大蓄水量是108.32亿立方米
四.函数概念与基本初等函数Ⅱ(三角函数的有关概念B;同角三角函数的基本关系式B;正弦、余弦的诱导公式B;正弦函数、余弦函数、正切函数的图象和性质B;函数 的图象和性质A;两角和(差)的正弦、余弦、和正切C;二倍角的正弦、余弦和正切B;积化和差、和差化积、半角公式A)
的图象和性质A;两角和(差)的正弦、余弦、和正切C;二倍角的正弦、余弦和正切B;积化和差、和差化积、半角公式A)
10.函数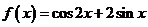 的最小值和最大值分别为
的最小值和最大值分别为 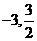
11.已知函数 (
( ,
,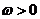 )为偶函数,且函数
)为偶函数,且函数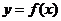 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为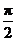 .
.
(Ⅰ)求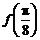 的值;
的值;
(Ⅱ)将函数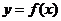 的图象向右平移
的图象向右平移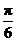 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数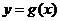 的图象,求
的图象,求 的单调递减区间.
的单调递减区间.
解:(Ⅰ)
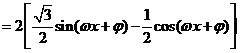
 .
.
因为 为偶函数,所以对
为偶函数,所以对 ,
,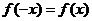 恒成立,
恒成立,
因此 .
.
即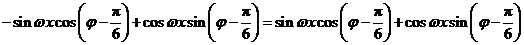 ,
,
整理得 .因为
.因为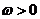 ,且
,且 ,所以
,所以 .
.
又因为 ,故
,故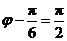 .所以
.所以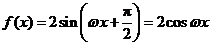 .
.
由题意得 ,所以
,所以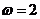 .故
.故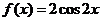 .因此
.因此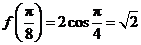 .
.
(Ⅱ)将 的图象向右平移
的图象向右平移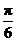 个单位后,得到
个单位后,得到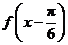 的图象,
的图象,
所以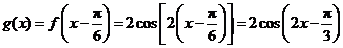 .
.
当 (
(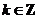 ),
),
即 (
(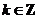 )时,
)时, 单调递减,
单调递减,
因此 的单调递减区间为
的单调递减区间为 (
(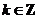 ).
).
 12.如图,某地有三家工厂,分别位于矩形ABCD的两个顶点A,B及CD的中点P处.AB=
12.如图,某地有三家工厂,分别位于矩形ABCD的两个顶点A,B及CD的中点P处.AB=
(1)按下列要求建立函数关系式:
(Ⅰ)设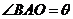 (rad),将
(rad),将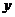 表示成
表示成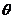 的函数;
的函数;
(Ⅱ)设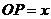 (km),将
(km),将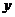 表示成
表示成 的函数;
的函数;
(3) 请你选用(1)中的一个函数关系确定污水处理厂的位置,使铺设的污水管道的总长度最短。
函数概念与基本初等函数Ⅱ(两角和(差)的正弦、余弦和正切;二倍角的正弦、余弦和正切;几个三角不等式)
解:(Ⅰ)①由条件知PQ 垂直平分AB,若∠BAO=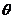 (rad) ,则
(rad) ,则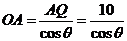 ,
,
故 ,又OP=
,又OP=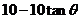 ,
,
所以 ,
,
所求函数关系式为
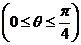
②若OP= (km) ,则OQ=10-
(km) ,则OQ=10- ,所以OA =OB=
,所以OA =OB=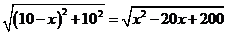
所求函数关系式为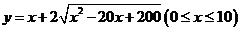
(Ⅱ)选择函数模型①,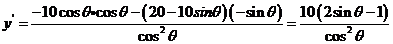
令 0 得sin
0 得sin  ,因为
,因为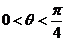 ,所以
,所以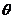 =
= ,
,
当 时,
时,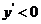 ,
,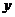 是
是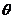 的减函数;
的减函数;
当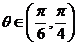 时,
时,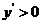 ,
,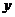 是
是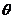 的增函数,所以当
的增函数,所以当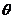 =
= 时,
时,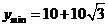 。
。
这时点P 位于线段AB 的中垂线上,在矩形区域内且距离AB 边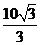 km处。
km处。
13.已知函数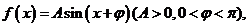
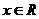 的最大值是1,其图象经过点M(
的最大值是1,其图象经过点M(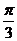 ,
,
(1)求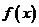 的解析式;(2)已知
的解析式;(2)已知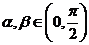 ,且
,且 ,求
,求 的值。
的值。
解析:(1)依题意有 ,则
,则 ,将点
,将点 代入得
代入得 ,
,
而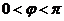 ,
,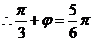 ,
,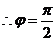 ,故
,故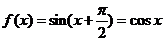 ;
;
(2)依题意有 ,而
,而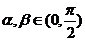 ,
,
 ,
,
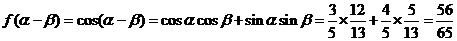 。
。
五.解三角形(正弦定理、余弦定理及其应用B)
14.满足条件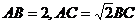 的三角形
的三角形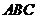 的面积的最大值
的面积的最大值
 15.
15.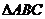 的三内角
的三内角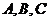 的对边边长分别为
的对边边长分别为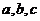 ,若
,若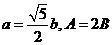 ,则
,则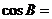
16.如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2。
(1)求cos∠CBE的值;(2)求AE。
解:(1) 因为
所以 ,
,
(2)在 中,
中,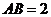 ,故由正弦定理得
,故由正弦定理得
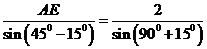 ,故
,故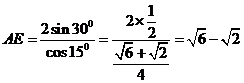
17.已知函数
 在
在 单调增加,在
单调增加,在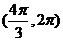 单调减少,则
单调减少,则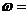
六.平面向量(平面向量的有关概念B;平面向量的加法、减法和数乘运算B;平面向量的坐标表示B;平面向量的数量积C;平面向量的平行与垂直B;平面向量的应用A)
18.已知四边形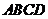 的三个顶点
的三个顶点 ,
, ,
,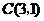 ,且
,且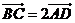 ,
,
则顶点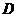 的坐标为
的坐标为 
19.已知平面向量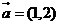 ,
,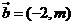 ,且
,且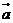 //
// ,则
,则 =
= 
20.已知 为
为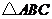 的三个内角
的三个内角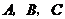 的对边,向量
的对边,向量
 .若
.若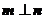 ,且
,且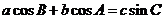 ,
,
则角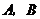 的大小分别为
的大小分别为 
21.设平面向量 ,若存在实数
,若存在实数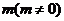 和角
和角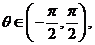 使向量
使向量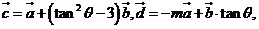 且
且
(1)求 的关系式;(2)若
的关系式;(2)若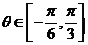 ,求
,求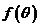 的最小值,并求出此时的
的最小值,并求出此时的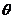 值。
值。
七.数列(数列的有关概念A;等差数列C;等比数列C)
22.将全体正整数排成一个三角形数阵:
|
 行(
行(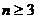 )从左向右的第3个数为
)从左向右的第3个数为 
 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表: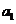

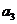


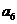


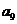
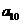
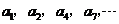 构成的
构成的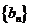 ,
, .
.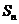 为数列
为数列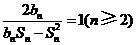 .
.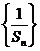 成等差数列,并求数列
成等差数列,并求数列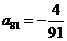 时,求上表中第
时,求上表中第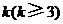 行所有项的和.
行所有项的和.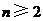 时,
时,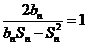 ,又
,又 ,
,

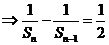 ,
,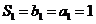 .所以数列
.所以数列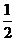 的等差数列.
的等差数列. ,
,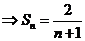 .
.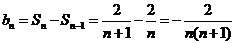 .
.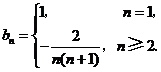
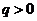 .
.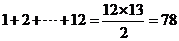 ,
,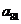 在表中第31行第三列,
在表中第31行第三列, .又
.又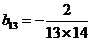 ,所以
,所以 .
.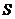 ,
,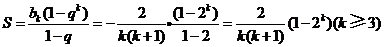 .
.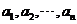 是各项均不为零的
是各项均不为零的 )项等差数列,且公差
)项等差数列,且公差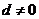 ,若将此数列删去某一项后得到的数列(按原来的顺序)是等比数列.
,若将此数列删去某一项后得到的数列(按原来的顺序)是等比数列.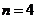 时,求
时,求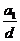 的数值;
的数值;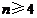 ),存在一个各项及公差均不为零的等差数列
),存在一个各项及公差均不为零的等差数列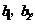
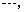
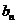 ,其中任意三项(按原来的顺序)都不能组成等比数列.
,其中任意三项(按原来的顺序)都不能组成等比数列.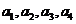 中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则推出d=0。
中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则推出d=0。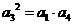 ,即
,即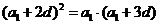 化简得
化简得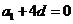 ,得
,得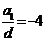
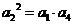 ,即
,即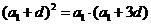 化简得
化简得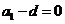 ,得
,得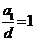
 中同样不可能删去
中同样不可能删去 ,否则出现连续三项。
,否则出现连续三项。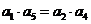 ,即
,即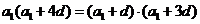 化简得
化简得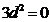 ,因为
,因为 ,所以
,所以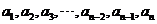 中,由于不能删去首项或末项,若删去
中,由于不能删去首项或末项,若删去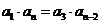 ,这与
,这与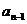 也有
也有 中任意一个,则必有
中任意一个,则必有 ,这与
,这与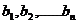 ,
, (
( )为任意三项成等比数列,则
)为任意三项成等比数列,则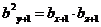 ,
,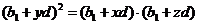 ,化简得
,化简得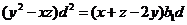 (*)
(*)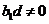 知,
知, 与
与 同时为0或同时不为0
同时为0或同时不为0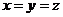 与题设矛盾。
与题设矛盾。
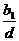 为有理数。
为有理数。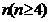 ,只要
,只要 ,
,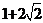 ,……,
,……, 满足要求。
满足要求。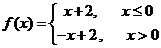 ,则不等式
,则不等式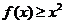 的解集是
的解集是
 为不等式组
为不等式组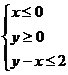 表示的平面区域,则当
表示的平面区域,则当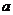 从-2连续变化到1时,动直线
从-2连续变化到1时,动直线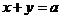 扫过
扫过 为实数。
为实数。 处取得极值,求
处取得极值,求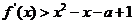 对任意
对任意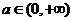 都成立,求实数
都成立,求实数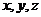 为正实数,满足
为正实数,满足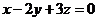 ,则
,则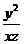 的最小值是 3
的最小值是 3 
 表示为
表示为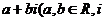 是虚数单位)的形式,则
是虚数单位)的形式,则 1 .
1 .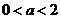 ,复数
,复数 的实部为
的实部为 的取值范围是
的取值范围是 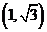
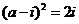 ,其中
,其中 是虚数单位,那么实数
是虚数单位,那么实数
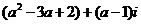 是纯虚数,则实数a的值为
是纯虚数,则实数a的值为
 等于
等于
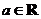 ,且
,且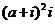 为正实数,则
为正实数,则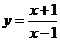 在点
在点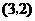 处的切线与直线
处的切线与直线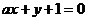 垂直,则
垂直,则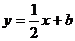 是曲线
是曲线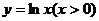 的一条切线,则实数
的一条切线,则实数 的值是
的值是 
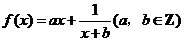 ,曲线
,曲线 处的切线方程为y=3.
处的切线方程为y=3.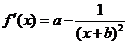 ,
, 解得
解得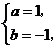 或
或
 ,故
,故 .
.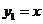 ,
,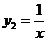 都是奇函数.
都是奇函数.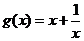 也是奇函数,其图像是以原点为中心的中心对称图形.而
也是奇函数,其图像是以原点为中心的中心对称图形.而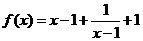 .可知,函数
.可知,函数 平移,即得到函数
平移,即得到函数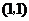 为中心的中心对称图形.
为中心的中心对称图形.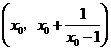 .
.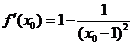 知,过此点的切线方程为
知,过此点的切线方程为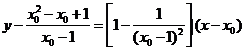 .
.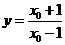 ,切线与直线
,切线与直线 .
. 令
令 得
得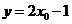 ,切线与直线
,切线与直线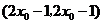 .
. .
.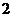 .
.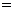 ”也可以写成“
”也可以写成“ ”或“
”或“ ”)
”)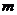 也整除
也整除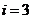 。
。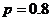 ,则输出的
,则输出的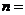 .
. ,因此输出
,因此输出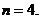
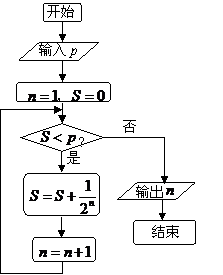 十二.常用逻辑用语(命题的四则运算法则A;必要条件、充分条件、
十二.常用逻辑用语(命题的四则运算法则A;必要条件、充分条件、 在其定义域内是减函数,
在其定义域内是减函数, ”的逆否命题是 ② (填序号)
”的逆否命题是 ② (填序号) ,则函数
,则函数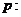 所有有理数都是实数,命题
所有有理数都是实数,命题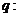 正数的对数都是负数,则下列命题中为真命题的是( D )
正数的对数都是负数,则下列命题中为真命题的是( D )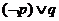 B.
B.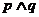 C.
C. D.
D.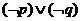
 为真命题,命题
为真命题,命题 为真命题
为真命题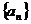 ,
,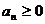 ,
,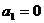 ,
,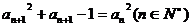 .
.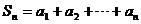 .
.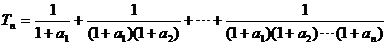 .
. 时,
时,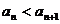 ;
; ;
;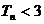 。
。 时,因为
时,因为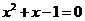 的正根,所以
的正根,所以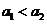 .
. 时,
时, ,
,

 ,
,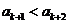 .
.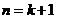 时,
时,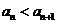 也成立.
也成立.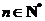 都成立.
都成立.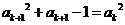 ,
, (
( ),
), .
. ,所以
,所以 .
.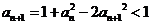 得
得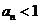 ,
,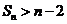 .
. ,得
,得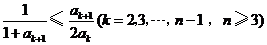
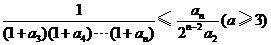 ,
, ,
,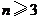 时,
时,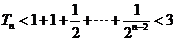 ,
,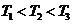 ,
,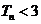 .
.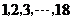 的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成以3为公差的等差数列的概率为
的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成以3为公差的等差数列的概率为
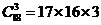 。能组成以3为公差的等差数列有(1,4,7),(2,5,8),
。能组成以3为公差的等差数列有(1,4,7),(2,5,8),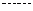 ,(12,15,18)共12组,因此概率
,(12,15,18)共12组,因此概率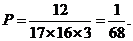
 与
与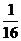 .
. ,求
,求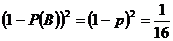
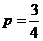 或
或 (舍去),所以乙投球的命中率为
(舍去),所以乙投球的命中率为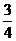
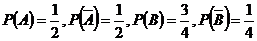

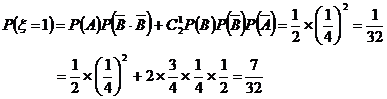
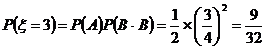
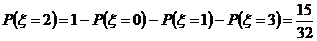
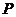
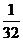
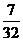
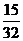
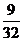

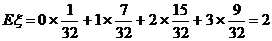
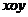 中,设
中,设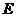 是到原点的距离不大于1的点构成的区域,向
是到原点的距离不大于1的点构成的区域,向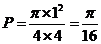
 三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为
三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为
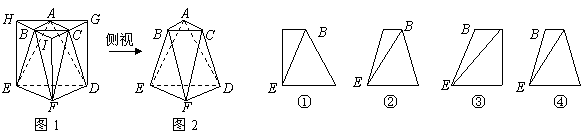

 解:从三视图可以看出该几何体是由一个球和一个圆柱组合而成的,其表面及为
解:从三视图可以看出该几何体是由一个球和一个圆柱组合而成的,其表面及为 
 ,点
,点 分别是
分别是 的中点.
的中点. 面
面 ;
; (2)平面
(2)平面 面
面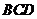 .
. 面ACD,AD
面ACD,AD 面ACD,∴直线EF∥面ACD;
面ACD,∴直线EF∥面ACD; 中,平面
中,平面 平面
平面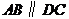 ,
,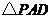 是等边三角形,已知
是等边三角形,已知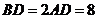 ,
,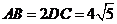 .
.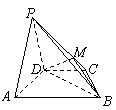 (Ⅰ)设
(Ⅰ)设 是
是 上的一点,证明:平面
上的一点,证明:平面 平面
平面 ;
; 中,
中, ,
,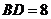 ,
,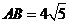 ,
,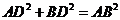 .故
.故 .
.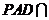 平面
平面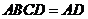 ,
,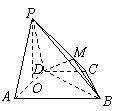
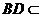 平面
平面 平面
平面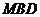 ,
,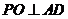 交
交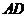 于
于 ,
,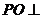 平面
平面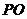 为四棱锥
为四棱锥 .
.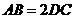 ,
,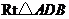 中,斜边
中,斜边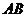 边上的高为
边上的高为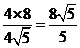 ,
,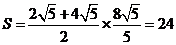 .
. 中,记二次函数
中,记二次函数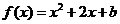 (
(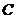 .
.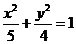 的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________
的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________ ,得交点
,得交点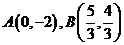 ;
;
 为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在
为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在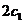 和
和 分别表示椭轨道Ⅰ和Ⅱ的焦距,用
分别表示椭轨道Ⅰ和Ⅱ的焦距,用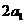 和
和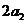 分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子: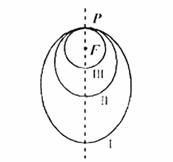 ①
①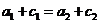 ; ②
; ②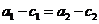 ;
③
;
③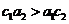 ; ④
; ④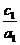 <
<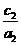 .
.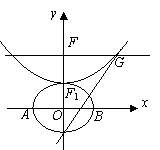 55.设
55.设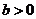 ,椭圆方程为
,椭圆方程为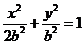 ,抛物线方程为
,抛物线方程为 .如图所示,过点
.如图所示,过点 作
作 ,已知抛物线在点
,已知抛物线在点 .
. 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标). ,
, 得
得 ,
, G点的坐标为
G点的坐标为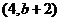 ,
,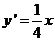 ,
, ,
, 即
即 ,
, 得
得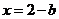 ,
, 点的坐标为
点的坐标为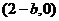 ,由椭圆方程得
,由椭圆方程得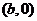 ,
,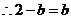 即
即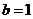 ,即椭圆和抛物线的方程分别为
,即椭圆和抛物线的方程分别为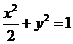 和
和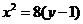 ;
; 过
过 为直角的
为直角的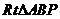 只有一个,
只有一个,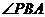 为直角的
为直角的 为直角,则点
为直角,则点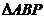 为直角三角形。
为直角三角形。