摘要：由知.与同时为0或同时不为0
网址：http://m.1010jiajiao.com/timu_id_101855[举报]
用α、β、γ三个字母组成一个长度为（n+1）（n∈N*）个字母的字符串，要求由α开始，相邻两个字母不同．例如：n=1时，排出的字符串是αβ或αγ；n=2时，排出的字符串是αβα、αβγ、αγα、αγβ（如图）．若记这种（n+1）个字符串中，最后一个字母仍是α的字符串的个数为an，可知a1=0，a2=2，a3=2，a4=6，…，则数列{an}的第n项an与第n-1项an-1（n≥2，n∈N*） ．
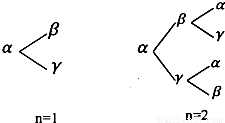查看习题详情和答案>>
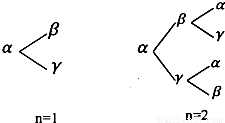查看习题详情和答案>>
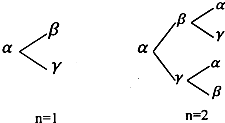（2012•安庆模拟）用α、β、γ三个字母组成一个长度为（n+1）（n∈N*）个字母的字符串，要求由α开始，相邻两个字母不同．例如：n=1时，排出的字符串是αβ或αγ；n=2时，排出的字符串是αβα、αβγ、αγα、αγβ（如图）．若记这种（n+1）个字符串中，最后一个字母仍是α的字符串的个数为an，可知a1=0，a2=2，a3=2，a4=6，…，则数列{an}的第n项an与第n-1项an-1（n≥2，n∈N*）an+an-1=2n-1，（n≥2）
an+an-1=2n-1，（n≥2）
．
已知点P是直角坐标平面内的动点，点P到直线l1：x=-2的距离为d1，到点F（-1，0）的距离为d2，且
=
．
（1）求动点P所在曲线C的方程；
（2）直线l过点F且与曲线C交于不同两点A、B（点A或B不在x轴上），分别过A、B点作直线l1：x=-2的垂线，对应的垂足分别为M、N，试判断点F与以线段MN为直径的圆的位置关系（指在圆内、圆上、圆外等情况）；
（3）记S1=S△FAM，S2=S△FMN，S3=S△FBN（A、B、M、N是（2）中的点），问是否存在实数λ，使S22=λS1S3成立．若存在，求出λ的值；若不存在，请说明理由．
进一步思考问题：若上述问题中直线l1：x=-
、点F（-c，0）、曲线C：
+
=1(a＞b＞0，c=
)，则使等式S22=λS1S3成立的λ的值仍保持不变．请给出你的判断 （填写“不正确”或“正确”）（限于时间，这里不需要举反例，或证明）．
查看习题详情和答案>>
| d2 |
| d1 |
| ||
| 2 |
（1）求动点P所在曲线C的方程；
（2）直线l过点F且与曲线C交于不同两点A、B（点A或B不在x轴上），分别过A、B点作直线l1：x=-2的垂线，对应的垂足分别为M、N，试判断点F与以线段MN为直径的圆的位置关系（指在圆内、圆上、圆外等情况）；
（3）记S1=S△FAM，S2=S△FMN，S3=S△FBN（A、B、M、N是（2）中的点），问是否存在实数λ，使S22=λS1S3成立．若存在，求出λ的值；若不存在，请说明理由．
进一步思考问题：若上述问题中直线l1：x=-
| a2 |
| c |
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
=0，直线AE与BF交于点P(x0，y0)，求证：
为定值;
(或
)，若存在，求出此时点E的坐标；若不存在，说明理由.