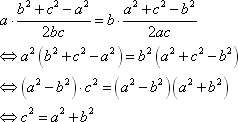摘要：(2)在中..故由正弦定理得
网址：http://m.1010jiajiao.com/timu_id_101806[举报]
已知
中，
，
.设
，记
.
（1） 求
的解析式及定义域；
（2）设
，是否存在实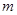数
，使函数
的值域为
？若存在，求出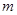的值；若不存在，请说明理由.
【解析】第一问利用（1）如图，在
中，由
，，
可得
，
又AC=2，故由正弦定理得
（2）中
由
可得
.显然，
，则
1
当m>0的值域为
m+1=3/2,n=1/2
2当m<0，不满足
的值域为；
因而存在实数m=1/2的值域为.
查看习题详情和答案>>
给出问题：已知
满足
，试判定的形状.某学生的解答如下：
解：（i）由余弦定理可得，
，
，
,
故
是直角三角形.
（ii）设外接圆半径为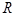
.由正弦定理可得，原式等价于
，
故是等腰三角形.
综上可知，是等腰直角三角形.
请问：该学生的解答是否正确？若正确，请在下面横线中写出解题过程中主要用到的思想方法；若不正确，请在下面横线中写出你认为本题正确的结果. .
查看习题详情和答案>>
给出问题：已知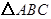
满足
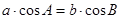，试判定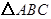的形状.某学生的解答如下：
解：（i）由余弦定理可得，
，
，
,
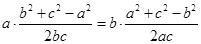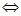
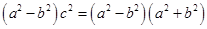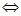
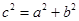故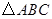
是直角三角形.
（ii）设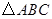外接圆半径为
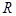.由正弦定理可得，原式等价于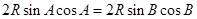
，
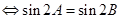
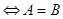故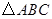是等腰三角形.
综上可知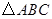，是等腰直角三角形.
请问：该学生的解答是否正确？若正确，请在下面横线中写出解题过程中主要用到的思想方法；若不正确，请在下面横线中写出你认为本题正确的结果. .
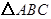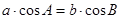满足，试判定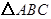的形状.某学生的解答如下：解：（i）由余弦定理可得，
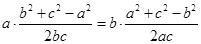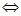
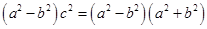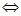
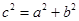，，,故
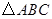是直角三角形.（ii）设
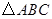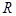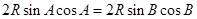
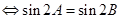
外接圆半径为.由正弦定理可得，原式等价于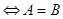，故
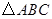是等腰三角形.综上可知，
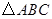是等腰直角三角形.请问：该学生的解答是否正确？若正确，请在下面横线中写出解题过程中主要用到的思想方法；若不正确，请在下面横线中写出你认为本题正确的结果. .
