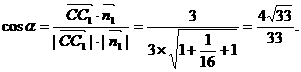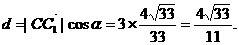12. (本题满分12分)(2005年高考·湖南卷·理17文18)
(本题满分12分)(2005年高考·湖南卷·理17文18)
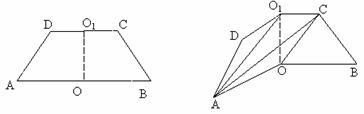
如图1,已知ABCD是上.下底边长分别为2和6,高为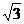 的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.
的等腰梯形,将它沿对称轴OO1折成直二面角,如图2.
(Ⅰ)证明:AC⊥BO1;
(Ⅱ)求二面角O-AC-O1的大小.
解法一(I)证明 由题设知OA⊥OO1,OB⊥OO1.
所以∠AOB是所折成的直二面角的平面角,
即OA⊥OB. 故可以O为原点,OA、OB、OO1
所在直线分别为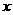 轴、y轴、z轴建立空间直角坐标系,
轴、y轴、z轴建立空间直角坐标系,
如图3,则相关各点的坐标是A(3,0,0),
B(0,3,0),C(0,1,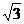 )
)
|
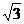 ).
).
从而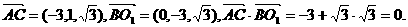
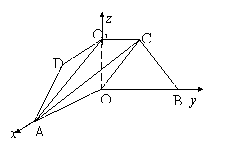 所以AC⊥BO1.
所以AC⊥BO1.
(II)解:因为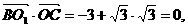 所以BO1⊥OC,
所以BO1⊥OC,
由(I)AC⊥BO1,所以BO1⊥平面OAC,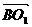 是平面OAC的一个法向量.
是平面OAC的一个法向量.
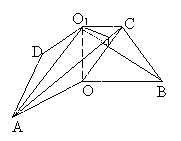 设
设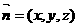 是0平面O1AC的一个法向量,
是0平面O1AC的一个法向量,
由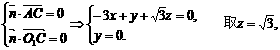 得
得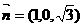 .
.
设二面角O-AC-O1的大小为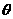 ,由
,由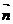 、
、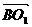 的方向可知
的方向可知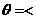
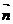 ,
,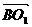 >,
>,
所以cos
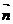 ,
,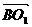 >=
>=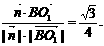
即二面角O-AC-O1的大小是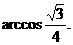
解法二(I)证明 由题设知OA⊥OO1,OB⊥OO1,
所以∠AOB是所折成的直二面角的平面角,
|
OC是AC在面OBCO1内的射影.
因为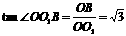
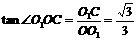 ,
,
所以∠OO1B=60°,∠O1OC=30°,从而OC⊥BO1
由三垂线定理得AC⊥BO1.
(II)解 由(I)AC⊥BO1,OC⊥BO1,知BO1⊥平面AOC.
设OC∩O1B=E,过点E作EF⊥AC于F,连结O1F(如图4),则EF是O1F在平面AOC
内的射影,由三垂线定理得O1F⊥AC.
所以∠O1FE是二面角O-AC-O1的平面角.
由题设知OA=3,OO1=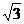 ,O1C=1,
,O1C=1,
所以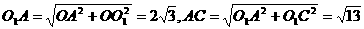 ,
,
从而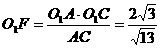 , 又O1E=OO1·sin30°=
, 又O1E=OO1·sin30°=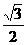 ,
,
所以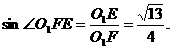 即二面角O-AC-O1的大小是
即二面角O-AC-O1的大小是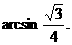
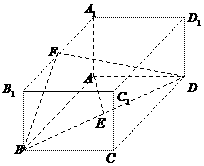 如图,已知长方体
如图,已知长方体

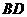 与平面
与平面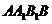 所成的角为
所成的角为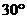 ,
,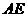 垂直
垂直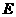 ,
, 为
为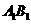 的中点.
的中点.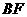 所成的角;
所成的角;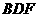 与平面
与平面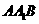 所成的二面角;
所成的二面角; 到平面
到平面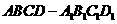 中,以
中,以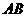 所在的直线为
所在的直线为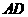 所在的直线为
所在的直线为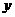 轴,
轴,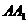 所在的直线为
所在的直线为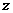 轴建立如图示空间直角坐标系
轴建立如图示空间直角坐标系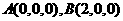 ,
,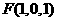
 平面
平面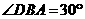 ,又
,又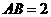 ,
,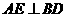 ,
,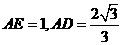 从而易得
从而易得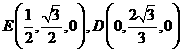
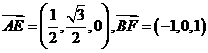 所以
所以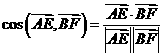 =
=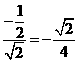
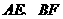 所成的角为
所成的角为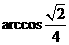
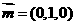 设
设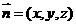 是平面
是平面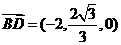 由
由
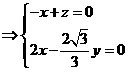
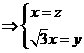
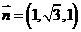 所以
所以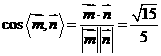 即平面
即平面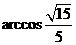
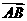 在平面
在平面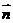 上的投影的绝对值,
上的投影的绝对值,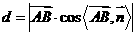 =
=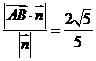 所以点
所以点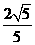
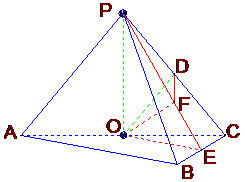
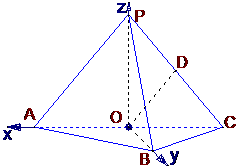
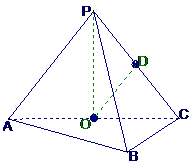
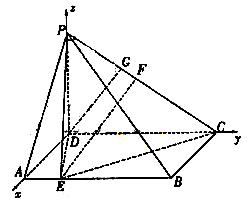
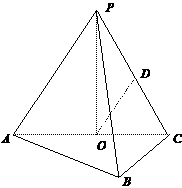 (2005年高考·浙江卷·文18)如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=
(2005年高考·浙江卷·文18)如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=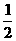 PA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
PA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
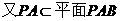
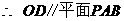
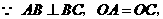
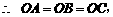
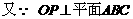
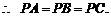
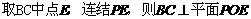
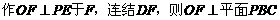
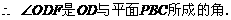
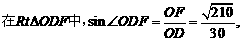
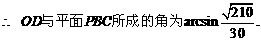

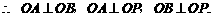
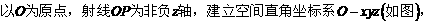
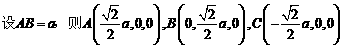
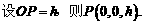
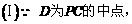
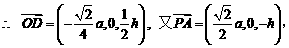
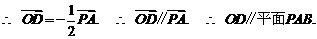
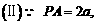

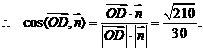
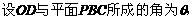
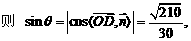
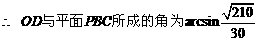
 (Ⅰ)当k=
(Ⅰ)当k=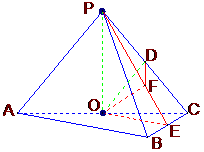
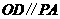 ,
, PA与平面PBC所成的角的大小等于
PA与平面PBC所成的角的大小等于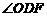 ,
,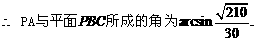
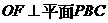 ,∴F是O在平面PBC内的射影
,∴F是O在平面PBC内的射影
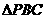 的重心,则B,F,D三点共线,
的重心,则B,F,D三点共线,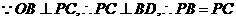 ,即
,即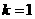
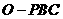 为正三棱锥,
为正三棱锥,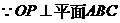 ,
,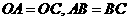 ,
,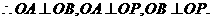
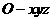 (如图)
(如图) 设
设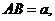 则
则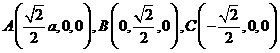 ,
,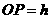 ,则
,则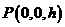
 D为PC的中点,
D为PC的中点,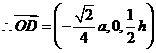 ,
,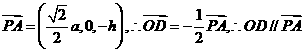 ,
,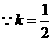 ,即
,即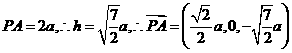 ,
,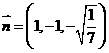 ,
,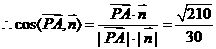 ,
,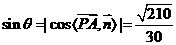 ,
,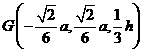 ,
,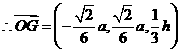 ,
,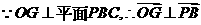 ,
,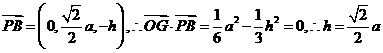 ,
,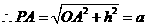 ,即
,即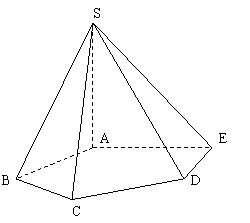

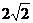 ,同理SE=
,同理SE=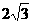 ,从而,cos∠SBE=
,从而,cos∠SBE=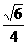 ,∴∠SBE=arccos
,∴∠SBE=arccos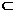 底面ABCDE,
底面ABCDE,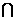 BA=A,∴BC⊥平面SAB。
BA=A,∴BC⊥平面SAB。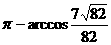 。
。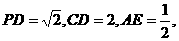 求
求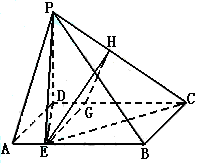 EC⊥DE,因此DE是异面直线PD与EC的公垂线.
EC⊥DE,因此DE是异面直线PD与EC的公垂线.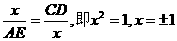 (负根舍去).
(负根舍去).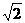 ,CD=2,GC=
,CD=2,GC=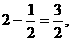
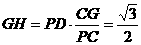 ,
,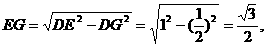

 (Ⅰ)以D为原点,
(Ⅰ)以D为原点,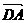 、
、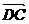 、
、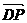 分别为x、y、z轴建立空间直角坐标系.
分别为x、y、z轴建立空间直角坐标系.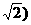 ,
,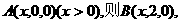
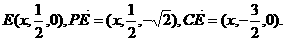 由
由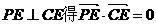 ,
,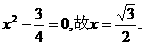 由
由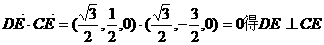 ,
,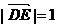 ,故异面直线PD、
,故异面直线PD、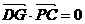 得
得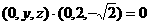
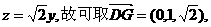 作EF⊥PC于F,设F(0,m,n),
作EF⊥PC于F,设F(0,m,n),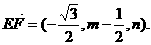
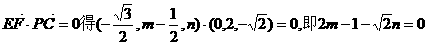 ,
,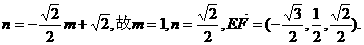
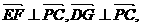 故平面E-PC-D的平面角
故平面E-PC-D的平面角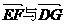 的夹角.
的夹角.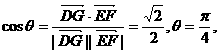 即二面角E-PC-D的大小为
即二面角E-PC-D的大小为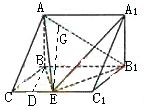
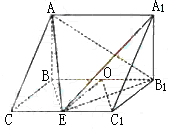
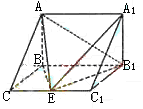 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB=
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB=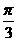 ,求:
,求: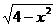 ,
,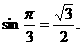
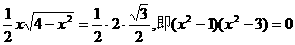 .
.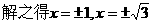 (负根舍去)
(负根舍去)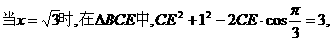
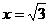 .
.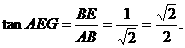
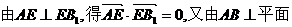
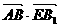 =0.
=0.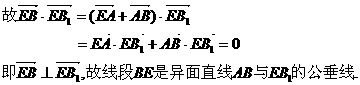
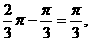 故△OC1E是正三角形,
故△OC1E是正三角形,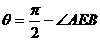 ,故
,故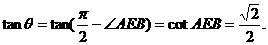
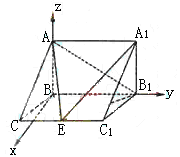 (I)以B为原点,
(I)以B为原点,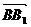 、
、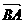 分别为y、z轴建立空间直角坐标系.
分别为y、z轴建立空间直角坐标系.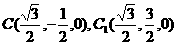
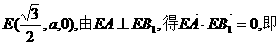
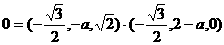
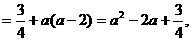
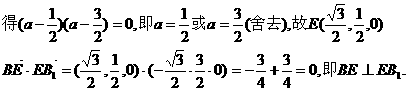
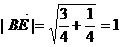 ,故异面直线AB、EB1的距离为1.
,故异面直线AB、EB1的距离为1.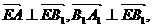 故二面角A-EB1-A1的平面角
故二面角A-EB1-A1的平面角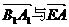 的夹角.
的夹角.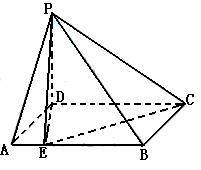
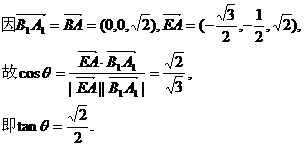
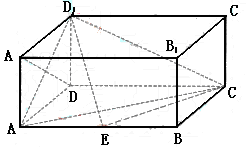 (本小题满分12分)(2005年高考·江西卷·理20文20)如图,在长方体ABCD-A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.(1)证明:D1E⊥A1D;
(本小题满分12分)(2005年高考·江西卷·理20文20)如图,在长方体ABCD-A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AB上移动.(1)证明:D1E⊥A1D;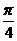 .
.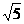 ,AD1=
,AD1=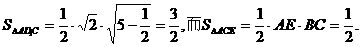
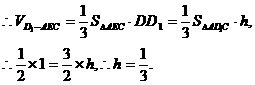
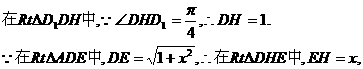

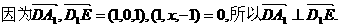
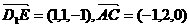 ,
,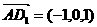 ,设平面ACD1的法向量为
,设平面ACD1的法向量为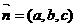 ,则
,则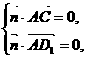
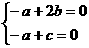 ,得
,得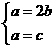 ,从而
,从而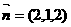 ,所以点E到平面AD1C的距离为
,所以点E到平面AD1C的距离为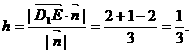
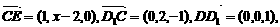
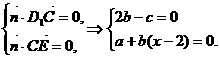 令b=1, ∴c=2,a=2-x,
令b=1, ∴c=2,a=2-x,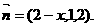
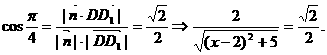
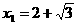 (不合,舍去),
(不合,舍去),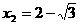 .
.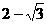 时,二面角D1-EC-D的大小为
时,二面角D1-EC-D的大小为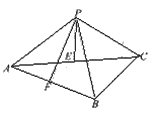 (本小题满分12分)(2005年高考·辽宁卷17)
(本小题满分12分)(2005年高考·辽宁卷17)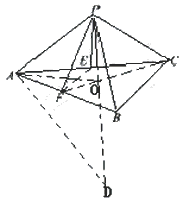 查空间想象能力及运用方程解未知量的基本方法,满分12分.
查空间想象能力及运用方程解未知量的基本方法,满分12分.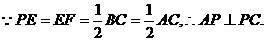
 ……4分
……4分
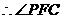 为所求二面角的平面角. 设AB=a,则AB=a,则
为所求二面角的平面角. 设AB=a,则AB=a,则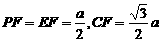
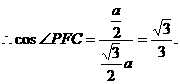 ……………………8分
……………………8分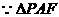 ≌
≌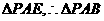 ≌
≌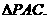
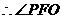 为所求二面角的平面角.
为所求二面角的平面角.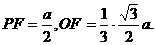
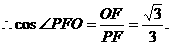 …………8分
…………8分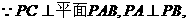
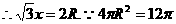 ,
,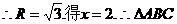 的边长为
的边长为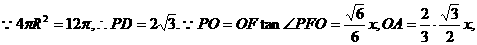
 .……12分
.……12分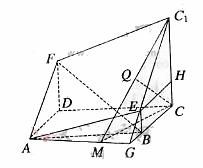 本小题主要考查线面关系和空间距离的求法等基础知识,同时考查空间想象能力和推理运算能力.
本小题主要考查线面关系和空间距离的求法等基础知识,同时考查空间想象能力和推理运算能力.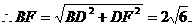
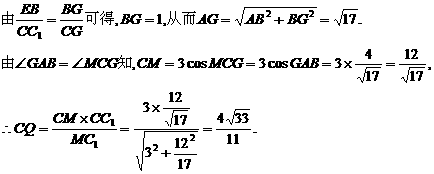
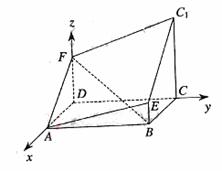 解法2:(I)建立如图所示的空间直角坐标系,则D(0,0,0),B(2,4,0),A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3).设F(0,0,z).
解法2:(I)建立如图所示的空间直角坐标系,则D(0,0,0),B(2,4,0),A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3).设F(0,0,z).
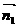 为平面AEC1F的法向量,
为平面AEC1F的法向量,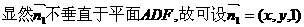
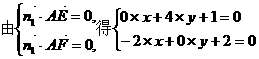
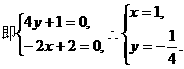
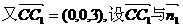 的夹角为a,则
的夹角为a,则