0 49776 49784 49790 49794 49800 49802 49806 49812 49814 49820 49826 49830 49832 49836 49842 49844 49850 49854 49856 49860 49862 49866 49868 49870 49871 49872 49874 49875 49876 49878 49880 49884 49886 49890 49892 49896 49902 49904 49910 49914 49916 49920 49926 49932 49934 49940 49944 49946 49952 49956 49962 49970 447348
 (本小题满分12分)(2005年高考·湖北卷·理20)
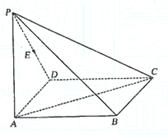
(本小题满分12分)(2005年高考·湖北卷·理20)  ,BC=1,PA=2,E为PD的中点. (Ⅰ)求直线AC与PB所成角的余弦值;
,BC=1,PA=2,E为PD的中点. (Ⅰ)求直线AC与PB所成角的余弦值;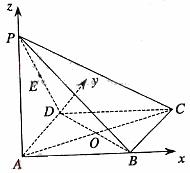 则A、B、C、D、P、E的坐标为A(0,0,0)、
则A、B、C、D、P、E的坐标为A(0,0,0)、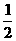 ,1),
,1),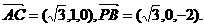
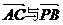 的夹角为θ,则
的夹角为θ,则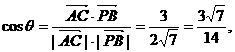
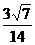 .
.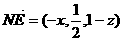 ,由NE⊥面PAC可得,
,由NE⊥面PAC可得,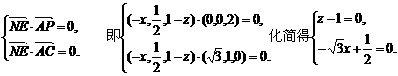 ∴
∴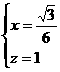
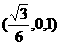 ,从而N点到AB、AP的距离分别为1,
,从而N点到AB、AP的距离分别为1,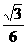 .
.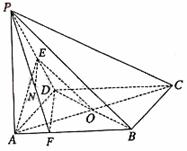 ∴∠EOA即为AC与PB所成的角或其补角.
∴∠EOA即为AC与PB所成的角或其补角.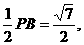
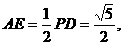
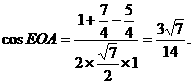
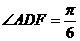 .
.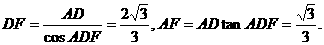
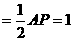 ,N点到AP的距离
,N点到AP的距离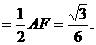
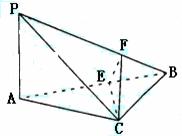 (本小题满分14分)(2005年高考·广东卷16)
(本小题满分14分)(2005年高考·广东卷16) .F是线段PB上一点,
.F是线段PB上一点, ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.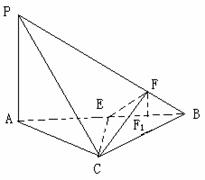 (I)证明:∵
(I)证明:∵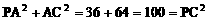 ,
,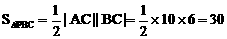 ,
,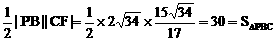 ,
,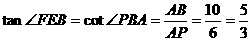 ,
,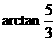 .
.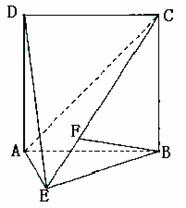 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.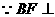 平面ACE.
平面ACE. 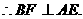
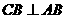 ,
, 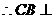 平面ABE.
平面ABE.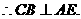
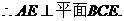
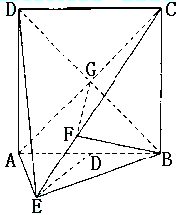 ∵正方形ABCD边长为2,∴BG⊥AC,BG=
∵正方形ABCD边长为2,∴BG⊥AC,BG=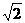 ,
,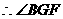 是二面角B-AC-E的平面角.
是二面角B-AC-E的平面角.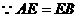 ,
, 直角
直角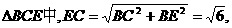
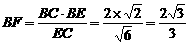 ,
,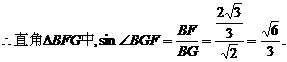
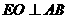 交AB于点O. OE=1.
交AB于点O. OE=1.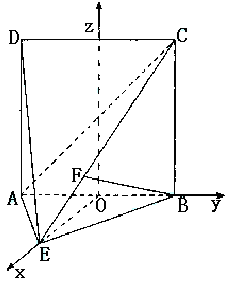 ∵二面角D-AB-E为直二面角,∴EO⊥平面ABCD.
∵二面角D-AB-E为直二面角,∴EO⊥平面ABCD.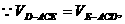
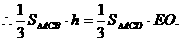
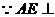 平面BCE,
平面BCE,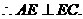
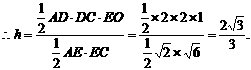

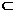 面BCE,
面BCE, 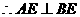 ,
,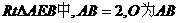 的中点,
的中点,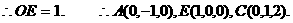
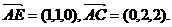 设平面AEC的一个法向量为
设平面AEC的一个法向量为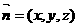 ,
,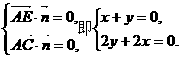
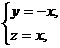
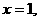 得
得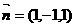 是平面AEC的一个法向量.
是平面AEC的一个法向量.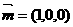 ,
,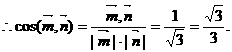
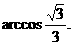
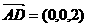 ,
,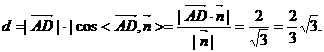
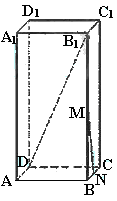 已知长方体
已知长方体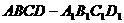 中,M、N分别是
中,M、N分别是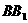 和BC的中点,AB=4,AD=2,
和BC的中点,AB=4,AD=2,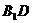 与平面ABCD所成角的大小为
与平面ABCD所成角的大小为 ,求异面直线
,求异面直线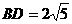 ,
,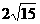 ,
,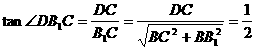
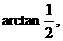
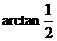 .
. (本题满分12分)(2005年高考·上海卷·理17)
(本题满分12分)(2005年高考·上海卷·理17)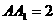 ,底面ABCD是直角梯形,∠A是直角,AB||CD,AB=4,AD=2,DC=1,求异面直线
,底面ABCD是直角梯形,∠A是直角,AB||CD,AB=4,AD=2,DC=1,求异面直线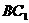 与DC所成角的大小.(结果用反三角函数值表示)
与DC所成角的大小.(结果用反三角函数值表示)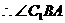 是异面直线BC1与DC所成的角.
是异面直线BC1与DC所成的角.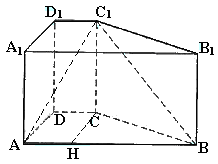 连结AC1与AC,在Rt△ADC中,可得
连结AC1与AC,在Rt△ADC中,可得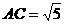 ,
,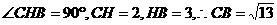
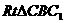 中,可得
中,可得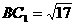 ,
,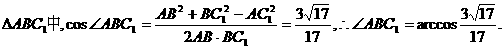
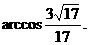
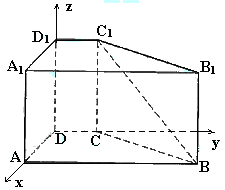 [解法二]如图,以D为坐标原点,分别以AD、DC、DD1所在直线为x、y、z轴建立直
[解法二]如图,以D为坐标原点,分别以AD、DC、DD1所在直线为x、y、z轴建立直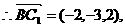
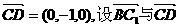 所成的角为
所成的角为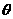 ,
,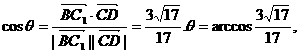
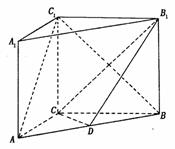 (本小题共14分)(2005年高考·北京卷·文16)
(本小题共14分)(2005年高考·北京卷·文16)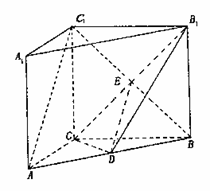 ∴AC⊥BC,且BC1在平面ABC内的射影为BC,
∴AC⊥BC,且BC1在平面ABC内的射影为BC,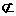 平面CDB1,
平面CDB1,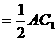 =
=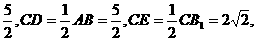
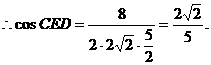
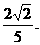
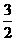 ,2,0).
,2,0).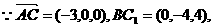
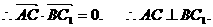
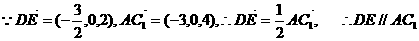

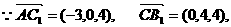
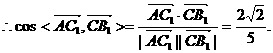
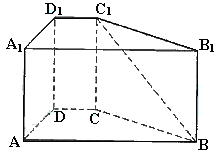
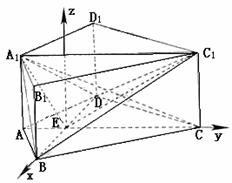
 如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=
如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=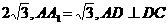 ,
,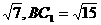 . 在△BFC1中,
. 在△BFC1中,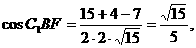
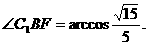
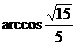 .
.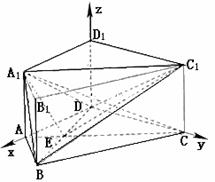 连结A1E,C1F,A1C1.
连结A1E,C1F,A1C1.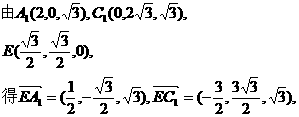

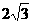 ,
,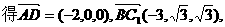
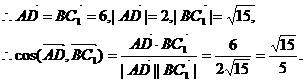
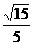 .
. 解法三:
解法三: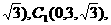
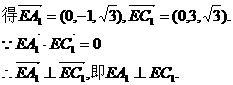
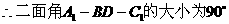 .
.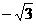 ,0,0),B(
,0,0),B(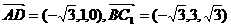 .
.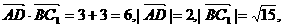
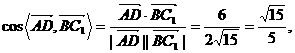
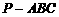 的体积为
的体积为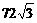 ,侧面与底面所成的二面角的大小为
,侧面与底面所成的二面角的大小为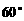 .
.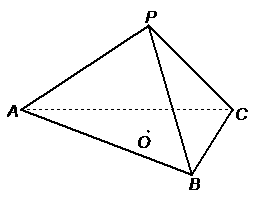 (1)证明:
(1)证明: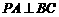 ;
;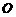 到侧面的距离.
到侧面的距离. 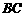 边的中点
边的中点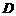 ,连接
,连接 、
、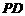 ,
,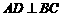 ,
,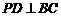 ,故
,故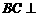 平面
平面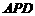 .
…… 4分
.
…… 4分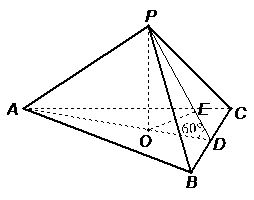 [解](2)如图, 由(1)可知平面
[解](2)如图, 由(1)可知平面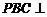 平面
平面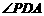 是侧面与底面所成二面角的平面角.
是侧面与底面所成二面角的平面角.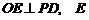 为垂足,则
为垂足,则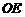 就是点
就是点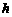 ,由题意可知点
,由题意可知点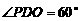 ,
,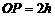 .
.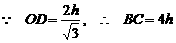 , …… 11分
, …… 11分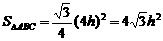 ,
,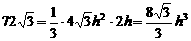 ,∴
,∴ 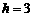 .
.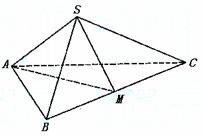 (本小题满分14分)(2005年春考·北京卷·文16)
(本小题满分14分)(2005年春考·北京卷·文16)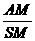 的值;
的值;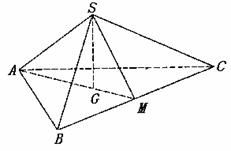 本小题主要考查直线与平面的位置关系等基本知识,考查空间想象能力,罗辑思维能力和运算能力.满分14分.
本小题主要考查直线与平面的位置关系等基本知识,考查空间想象能力,罗辑思维能力和运算能力.满分14分.
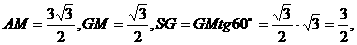
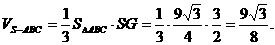
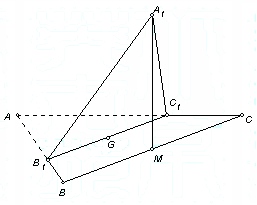 (本小题满分14分)(2005年春考·北京卷·理16)
(本小题满分14分)(2005年春考·北京卷·理16)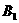 、
、 .将
.将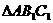 沿
沿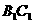 折起到
折起到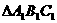 的位置,使点
的位置,使点 在平面
在平面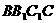 上的射影恰是线段BC的中点M.求:
上的射影恰是线段BC的中点M.求: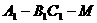 的大小;
的大小;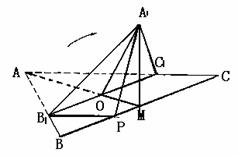 (2)异面直线
(2)异面直线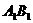 与
与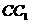 所成角的大小(用反三角函数表示).
所成角的大小(用反三角函数表示).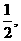 A1B1=AB1=2.
A1B1=AB1=2.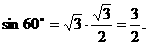
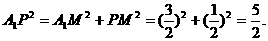
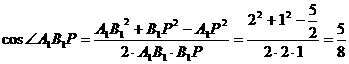 ,
,