摘要: (1) 由, 得 2分 由(1)得 m = , 当a = 2时, m = 2, 满足(2)式; 当a = 3时, m = 1, 不满足 = . 3分 (2) 由条件得 ∴ an(1 – an) = 2Sn (3) , 2分 令n = 1,得 a1 = –1, 又an – 1 (1 – an – 1 ) = 2S n – 1 , ∴( an + a n – 1 )( an + 1 – a n – 1 )= 0, 由an – a n – 1 = – 1 , a1 = –1,得{an}是首项为– 1, 公差为– 1的等差数列, ∴ an= – 1 + = – n . 3分 知,满足条件的数列不惟一. 考虑到a1 ¹ 1, 由 an = – a n – 1 及an – a n – 1 = – 1和a1 = –1, 构造数列{ –1, –2, 2,–2, –3, – 4, - , – n +2, - }. 2分 用数学归纳法证明,该数列满足(3)式, 当n = 1, 2, 3, 4, 5时,直接代入可得(3)式成立, 假设n = k 成立, 则n = k + 1时, Sk+1 =S k + a k+1 = ak(1 – ak) + a k + 1 = (–a k +1)(1 + ak+1) + a k + 1 =ak+1(1 – a k+1). 所以n = k + 1时(3)式成立, 即该数列满足题设条件. 得满足条件的数列不惟一. 构造数列也可能是: { –1, 1, –1, –2, –3, – 4, - , – n , - }; { –1, –2,2, –2, 2, –2, - , (–1) n – 1 2 , - } { –1, –2,2, –2, –3, – 4, - , – n , - }等等.
网址:http://m.1010jiajiao.com/timu3_id_498186[举报]
(本小题满分14分) 已知函数 ,(x>0).
,(x>0).
(1)当0<a<b,且f(a)=f(b)时,求 的值 ;
的值 ;
(2)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,求出a,b的值,若不存在,请说明理由.
(3)若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ma,mb],(m≠0),求m的取值范围.
查看习题详情和答案>>
(本小题满分14分)已知函数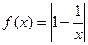 ,(x>0).
,(x>0).
(1)当0<a<b,且f(a)=f(b)时,求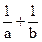 的值 ;
的值 ;
(2)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,求出a,b的值,若不存在,请说明理由.
(3) 若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [
若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ ma,mb],(m≠0),求m的取值范围.
ma,mb],(m≠0),求m的取值范围.
(本小题满分14分)如图9所示,流程图给出了无穷整数数列![]() 满足的条件,
满足的条件,![]() ,且当k=5时,输出的S=
,且当k=5时,输出的S=![]() ;当k=10时,输出的S=
;当k=10时,输出的S=![]() 。
。![]()
(1)试求数列![]() 的通项公式
的通项公式![]() ;(2)是否存在最小的正数M使得
;(2)是否存在最小的正数M使得![]() 对一切正整数n都成立,若存在,求出M的值;若不存在,请说明理由。
对一切正整数n都成立,若存在,求出M的值;若不存在,请说明理由。 ![]()
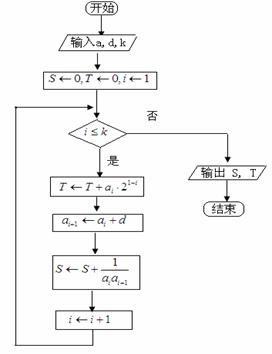
第22题图 图9
查看习题详情和答案>>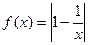 ,(x>0).
,(x>0).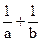 的值 ;
的值 ;  若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [
若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ ma,mb],(m≠0),求m的取值范围.
ma,mb],(m≠0),求m的取值范围.