摘要: 如图14-1至14-4中.两平行线AB,CD间的距离为6.点M为AB上一定点. 思考 如图14-1.圆心为O的半圆纸片在AB,CD之间.其直径MN在AB上.MN=8.点P为半圆上一点.设∠MOP=α. 当α= 度时.点P到CD的距离最小.最小值为 . 探究一 在图14-1的基础上.以点M为旋转中心.在AB,CD之间顺时针旋转该半圆纸片.直到不能再转动为止.如图14-2.得到最大旋转角∠BMO= 度.此时点N到CD的距离是 探究二 将图14-1中的扇形纸片NOP按下面对α要求剪掉.使扇形纸片MOP绕点M在AB,CD之间顺时针旋转. (1)如图14-3.当α=60°时.球在旋转过程中.点p到CD的最小距离.并请指出旋转角∠BMO的最大值, (2)如图14-4.在扇形纸片MOP旋转过程中.要保证点P能落在直线CD上.请确定α的取值范围. (参考数据:sin49°=,cos41°=.tan37°= ) [答案]思考 90.2, 探究一 30.2, 探究二 (1)由已知得M与P的距离为4.∴当MP⊥AB时.点P到AB的最大距离为4.从而点P到CD的最小距离为6-4=2.当扇形MOP在AB,CD之间旋转到不能再转时.弧MP与AB相切.此时旋转角最大.∠BMO的最大值为90°. (2)如图.由探究一可知.点P是弧MP与CD的切点时.α达到最大.即OP⊥CD.此时延长PO交AB于点H.α最大值为∠OMH+∠OHM=30°+90°=120°. 如图.当点P在CD上且与AB距离最小时.MP⊥CD,α达到最小.连接MP.作OH⊥MP于点H.由垂径定理.得MH=3.在Rt△MOH中.MO=4.∴sin∠MOH=.∴∠MOH=49°.∵α=2∠MOH.∴α最小值为98°.∴α的取值范围是98°≤α≤120°.
网址:http://m.1010jiajiao.com/timu3_id_496075[举报]
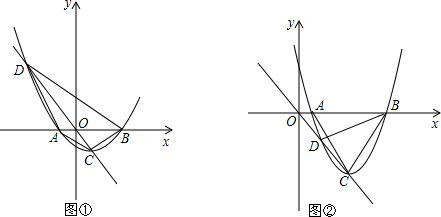
在直角坐标系xOy中,抛物线y=x2-2tx+t2-t(t>0)与x轴的两个交点分别为A、B(A在B的左边),直线l:y=kx经过抛物线的顶点C,与抛物线的另一个交点为D.
(1)求抛物线的顶点C的坐标(用含t的代数表示),并求出直线l 的解析式;
(2)如图①,当t=
时,探究AC与BD的位置关系,并说明理由;
(3)当t≠1时,设△ABC的面积为S1,△ABD的面积为S2,用含t的代数式表示
的值.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求抛物线的顶点C的坐标(用含t的代数表示),并求出直线l 的解析式;
(2)如图①,当t=
| 1 |
| 4 |
(3)当t≠1时,设△ABC的面积为S1,△ABD的面积为S2,用含t的代数式表示
| S1 |
| S2 |
 查看习题详情和答案>>
查看习题详情和答案>>
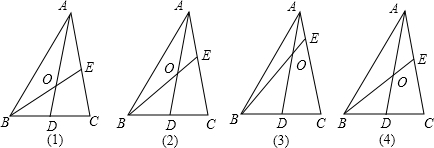
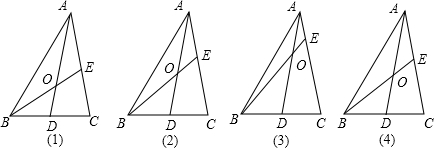
如图,在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD与点O,某学生在研究这一问题时,发现了如下事实,
①当
=
=
时,有
=
=
(如图1);
②当
=
=
时,有
=
=
(如图2);
③
=
=
时,有
=
=
(如图3);
如图4中,当
=
时,请你猜想
的一般结论,并证明你的结论(其中n为正整数).
 查看习题详情和答案>>
查看习题详情和答案>>
①当
| AE |
| AC |
| 1 |
| 2 |
| 1 |
| 1+1 |
| AO |
| AD |
| 2 |
| 3 |
| 2 |
| 2+1 |
②当
| AE |
| AC |
| 1 |
| 3 |
| 1 |
| 1+2 |
| AO |
| AD |
| 2 |
| 4 |
| 2 |
| 2+2 |
③
| AE |
| AC |
| 1 |
| 4 |
| 1 |
| 1+3 |
| AO |
| AD |
| 2 |
| 5 |
| 2 |
| 2+3 |
如图4中,当
| AE |
| AC |
| 1 |
| 1+n |
| AO |
| AD |
 查看习题详情和答案>>
查看习题详情和答案>>
自然数按如图规律排列,14这个数第4行,第三列,记作(4,3),那么69这个数位记作
1 2 5 10 17 ….
4 3 6 11 18 …
9 8 7 12 19 …
16 15 1 4 13 20 …
25 24 23 22 21 …
查看习题详情和答案>>
(5,9)
(5,9)
; 1218这个数位记作(35,8)
(35,8)
.1 2 5 10 17 ….
4 3 6 11 18 …
9 8 7 12 19 …
16 15 1 4 13 20 …
25 24 23 22 21 …