10.如图,在梯形ABCD中,AB//DC,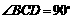 ,且AB=1,BC=2,tan∠ADC=2.
,且AB=1,BC=2,tan∠ADC=2.
 ⑴ 求证:DC=BC;
⑴ 求证:DC=BC;
|
⑶在⑵的条件下,当BE:CE=1:2,∠BEC= 时,求sin∠BFE的值.
时,求sin∠BFE的值.
解:(1)过A作DC的垂线AM交DC于M,
则AM=BC=2. 又tan∠ADC=2, ∴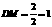 .
.
因为MC=AB=1, ∴DC=DM+MC=2即DC=BC.
(2)等腰直角三角形.
证明:∵ 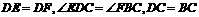 .
.
∴△DEC≌△BFC
∴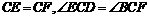 .
.
∴
即△ECF是等腰直角三角形.
(3)设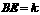 ,则
,则 , ∴
, ∴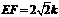 .
.
∵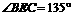 ,又
,又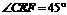 ,∴
,∴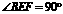 .
.
∴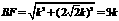 ,
,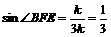 .
.
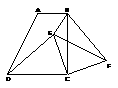
9.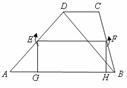 如图,梯形
如图,梯形 中,
中,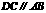 ,
, 是中位线,
是中位线,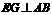 于
于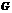 ,
,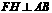 于
于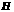 ,梯形的高
,梯形的高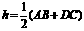 .沿着
.沿着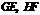 分别把
分别把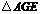 ,
, 剪开,然后按图中箭头所指方向,分别绕着点
剪开,然后按图中箭头所指方向,分别绕着点 旋转
旋转 ,将会得到一个什么样的四边形?简述理由.
,将会得到一个什么样的四边形?简述理由.
|
解:将会得到一个正方形,理由如下:
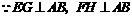 ,
,
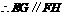 .
.
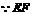 是梯形
是梯形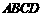 的中位线,
的中位线,
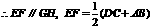 ,
,
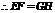 .
.
 梯形的高
梯形的高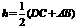 ,
,
 梯形的高
梯形的高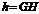 .
.
设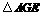 绕点
绕点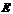 旋转
旋转 后点
后点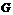 落在
落在 处,
处,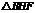 绕点
绕点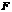 旋转
旋转 后,点
后,点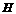 落在
落在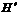 处则
处则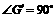 ,
,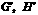 在
在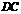 所在的直线上.
所在的直线上.
 是梯形
是梯形 的高.
的高.
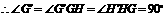 ,
,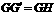 .
.
 四边形
四边形 是正方形.
是正方形.
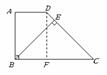
8.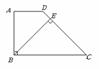 (2006 北京)已知:如图,在梯形
(2006 北京)已知:如图,在梯形 中,
中,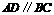 ,
,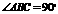 ,
,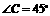 ,
,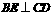 于点
于点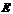 ,
,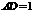 ,
,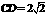 .
.
求: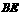 的长.
的长.
|
解:如图,过点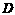 作
作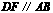 交
交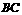 于点
于点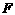 .
.
∵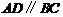 ,
,
 ∴四边形
∴四边形 是平行四边形.
是平行四边形.
∴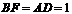 .
.
由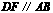 ,
,
得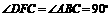 .
.
在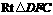 中,
中,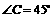 ,
,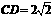 ,
,
由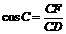 , 求得
, 求得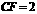 .
.
∴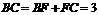 .
.
在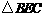 中,
中,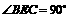 ,
,
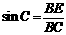 .求得
.求得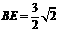 .
.
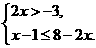 的最小整数解是( )
的最小整数解是( )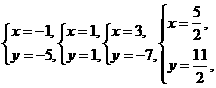 四对数值中,满足方程3x-y=2的有( )
四对数值中,满足方程3x-y=2的有( )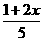 ≤1的解集在数轴上(图3-1)表示正确的是( )
≤1的解集在数轴上(图3-1)表示正确的是( )