摘要：10．如图.在梯形ABCD中.AB//DC..且AB=1.BC=2.tan∠ADC=2. ⑴ 求证:DC=BC, ⑵ E是梯形内的一点.F是梯形外的一点.且∠EDC=∠FBC.DE=BF.试判断△ECF的形状.并证明你的结论, ⑶在⑵的条件下.当BE:CE=1:2.∠BEC=时.求sin∠BFE的值． 解:(1)过A作DC的垂线AM交DC于M, 则AM=BC=2. 又tan∠ADC=2, ∴. 因为MC=AB=1, ∴DC=DM+MC=2即DC=BC. (2)等腰直角三角形. 证明:∵ . ∴△DEC≌△BFC ∴. ∴ 即△ECF是等腰直角三角形. (3)设,则. ∴. ∵.又.∴. ∴.．
网址：http://m.1010jiajiao.com/timu3_id_457223[举报]
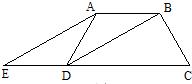20、如图，在梯形ABCD中，AB∥DC，DB平分∠ADC，过点A作AE∥BD，交CD的延长线于点E，且∠C=2∠E．（1）求证：梯形ABCD是等腰梯形；
（2）若∠BDC=30°，AD=5，求CD的长．
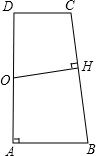如图，在梯形ABCD中，AB∥DC，∠A=90°，且AB=4，CD=3，BC=7．O为AD边的中点，OH⊥BC于H，求OH的长．
26、如图，在梯形ABCD中，AB∥DC，DB平分∠ADC，过点A作AE∥BD，交CD的延长线于点E，且∠C=2∠E．梯形ABCD是等腰梯形吗？请说明理由．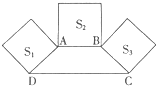
31、如图，在梯形ABCD中，AB∥DC，∠ADC+∠BCD=90°，且DC=2AB，分别以DA、AB、BC为边向梯形外作正方形，其面积分别为S1、S2、S3，请你探索S1、S2、S3之间的关系并说明理由．
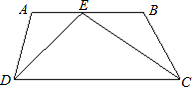23、如图，在梯形ABCD中，AB∥DC，∠ADC的平分线交AB于点E，且AB=AD+BC．