2、画图题:(写画法,保留画图的痕迹)
① 如图11-25,画出△ABC绕AB中点O逆时针旋转90°后的三角形。
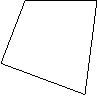
② 如图11-26,已知四边形ABCD和图形外一点O,画出四边形ABCD关于点O成中心对称的图形。
C
A
O  O
OB 图11-25 |
 A
D
A
D
O B C 图11-26 |
 E EB
A C F 图11-27 |
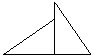
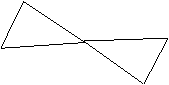
⒈如图11-23所示,要由等边△ABC得到等边△BDE,下列说法中正确的是( )
A.仅能由平移得到 B.仅能由旋转得到
C.既能由平移得到,又能由旋转得到 D.平移,旋转都不能得到
            
A. B. C. D. |
⒉ 如图所示,其中某图形中的一个矩形是另一个矩形顺时针方向旋转90°后所形成的,这个图形是( )。
⒊在26个大写英文字母中,既是轴对称图形,又是中心对称图形的有( )
A.3个 B.4个 C.5个 D.6个
⒋ 下列图形中,既是中心对称图形,又是轴对称图形的是( )
A.等边三角形 B.平行四边形 C.等腰梯形 D.圆
⒌ 要使正十边形旋转后与自身重合,至少应将它绕中心按逆时针方向旋转( )
A. 9° B. 18° C. 36° D. 72°
⒍ 你玩过扑克牌吗?你仔细观察过每张扑克牌中的图案吗?请你指出图案是中心对称图形的一组为( )。
A.黑桃6与黑桃9 B.红桃6与红桃9 C.梅花6与梅花9 D.方块6与方块9
 E
D E
DA B C 图11-24 |
⒈平移是由________所决定的。
⒉ 如图11-13所示,△ABC是由△DEF经过平移得到的,若AD=6cm,则 BE=______,CF=____,若M、N分别为AB、DE的中点,则MN=__________
       A D A DB M C N 图11-14 |
⒊ 如图11-14所示,四边形ABCD中,AD∥BC,DM∥AB交BC于M,DN∥AC交BC延长线于N,线段AD沿着___的方向平移到BM,平移的距离是______;线段AB沿着___的方向平移到DM,平移的距离为____;△ABC沿着___方向平移到△DMN,平移距离为_____。
     A D A DB C E F 图11-15 |
⒋ 如图11-15,将△ABC沿BC方向平移3cm得△DEF,若∠B=450,∠A=500,则∠F=___,BE=______=_______cm
⒌ 正方形至少旋转__度能与自身重合,正六边形至少旋转__度能与自身重合。正八边形至少旋转__度能与自身重合,
⒍ 成中心对称的两个图形,连结对称点的线段都经过__,并被______平分。
  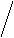   D
C D
CA E B 图11-17 |
  D
D E
EA B
C 图11-16 |
⒎ 如图11-16,△ABC与△ADE都是等腰直角三角形,如果△ABC经旋转后能与△ADE重合,那么旋转中心是_____,旋转了___度?
⒏ 钟表的分针匀速旋转一周需要60分,它的旋转中心是___,经过20分钟,分针旋转__度。
⒐ 如图11-17,在梯形ABCD中,AB∥CD,将BC沿CD方向平移6cm至ED,
△AED的周长为28cm,则梯形ABCD的周长为____cm.
      A E D A E DB F G C 图11-18 |
⒑ 已知梯形的两底长分别为6、8,一腰长为7,则另一腰长a的取值范围是_____;若a为奇数,则此时梯形为____梯形。
⒒ 如图11-18,四边形ABCD中 ,AD∥BC,BC>AD,∠B与∠C互余,将AB、CD分别平移到EF和EG的位置,则△EFG为_____三角形。若AD=2cm,BC=8cm,则FG=___cm。若AB=8cm,DC=6cm,则FG=___cm.
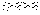 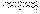    
图11-19 |
⒓ 如图11-19,一个矩形中有两个面积分别为9cm2和4cm2的正方形,则阴影部分面积为___。
 C
CA B O O D 图11-21 |
⒔、如图11-20:△OAC经旋转后与△OBD重合,则旋转中心是____________,旋转角是___________,若OC=3cm,则旋转过程中,点C所经过的路线长为_____________。
 A A
D C O 图11-20 B |
 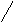  A
D A
D E E B
C B
CF 图11-22 |
⒕、将两直角三角尺的直角顶点重合为如图11-21所示的形状,若∠AOD=127°,
则∠BOC=__________。
⒖、如图11-22,E为正方形ABCD内一点,∠AEB=135°BE=3 cm,
△AEB按顺时针方向旋转一个角度后成为△CFB,△BEF是__________三角形,∠BFC=________度,BF=_________cm。
  C E C E A B D 图11-23 |
16.(2006郴州)如图1,矩形纸片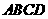 的边长分别为
的边长分别为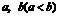 .将纸片任意翻折(如图2),折痕为
.将纸片任意翻折(如图2),折痕为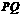 .(
.(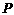 在
在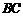 上),使顶点
上),使顶点 落在四边形
落在四边形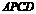 内一点
内一点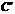 ,
, 的延长线交直线
的延长线交直线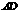 于
于 ,再将纸片的另一部分翻折,使
,再将纸片的另一部分翻折,使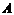 落在直线
落在直线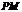 上一点
上一点 ,且
,且 所在直线与
所在直线与 所在直线重合(如图3)折痕为
所在直线重合(如图3)折痕为 .
.
(1)猜想两折痕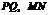 之间的位置关系,并加以证明.
之间的位置关系,并加以证明.
(2)若 的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕
的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕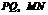 间的距离有何变化?请说明理由.
间的距离有何变化?请说明理由.
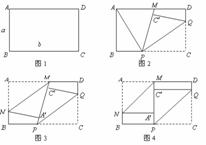 (3)若
(3)若 的角度在每次翻折的过程中都为
的角度在每次翻折的过程中都为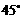 (如图4),每次翻折后,非重叠部分的四边形
(如图4),每次翻折后,非重叠部分的四边形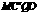 ,及四边形
,及四边形 的周长与
的周长与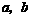 有何关系,为什么?
有何关系,为什么?
|
解:(1)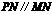 .
.
因为四边形 是矩形,所以
是矩形,所以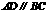 ,且
,且 在
在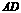 直线上,则有
直线上,则有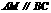
∴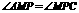 ,由翻折可得:
,由翻折可得: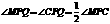 ,
,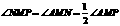 ,
,
∴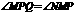 ,故
,故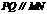 .
.
(2)两折痕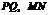 间的距离不变
间的距离不变
过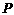 作
作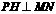 ,则
,则 ,
,
 因为
因为 的角度不变,所以
的角度不变,所以 的角度也不变,则所有的
的角度也不变,则所有的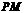 都是平行的.
都是平行的.
又因为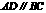 ,所以所有的
,所以所有的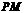 都是相等的
都是相等的
又因为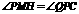 ,
,
故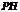 的长不变.
的长不变.
(3)当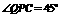 时,四边形
时,四边形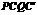 是正方形,
是正方形,
四边形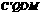 是矩形.因为
是矩形.因为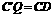 ,
,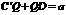 ,所以矩形
,所以矩形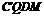 的周长为
的周长为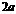 .
.
同理可得矩形 的周长为
的周长为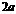 ,所以两个四边形的周长都为
,所以两个四边形的周长都为 ,与
,与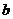 无关.
无关.
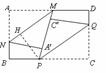
13.如图,在梯形 中,
中,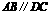 ,过对角线
,过对角线 的中点
的中点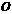 作
作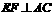 ,分别交边
,分别交边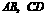 于点
于点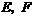 ,连接
,连接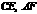 .
.
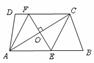 (1)求证:四边形
(1)求证:四边形 是菱形;
是菱形;
|
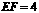 ,
,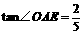 ,
,
求四边形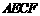 的面积.
的面积.
(1)证明:方法1: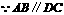 ,
,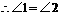 .
.
在 和
和 中,
中,
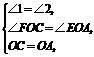
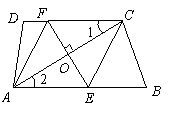
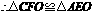 .
.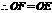 ,
,
又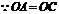 ,
, 四边形
四边形 是平行四边形.
是平行四边形.
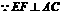 ,
, 四边形
四边形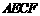 是菱形.
是菱形.
方法2:证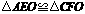 同方法1,
同方法1,
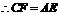 ,
,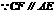 ,
, 四边形
四边形 是平行四边形.
是平行四边形. 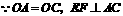 ,
,
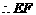 是
是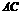 的垂直平分线,
的垂直平分线,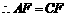 ,
,
 四边形
四边形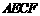 是菱形.
是菱形.
(2)解: 四边形
四边形 是菱形,
是菱形,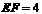 ,
,
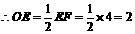 .
.
在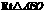 中,
中,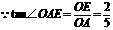 ,
,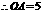 ,
,
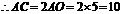 .
.
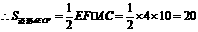 .
.
核心精神---创新关
12.)任意剪一个三角形纸片,如图中的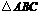 ,不妨设它的一个锐角为
,不妨设它的一个锐角为 ,首先利用对折的方法得到高
,首先利用对折的方法得到高 .然后按图中所示的方法分别将含有
.然后按图中所示的方法分别将含有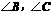 的部分向里折,找出
的部分向里折,找出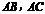 的中点
的中点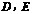 ,同时得到两条折痕
,同时得到两条折痕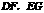 ,分别沿折痕
,分别沿折痕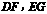 剪下图中的三角形①,②,并按图中箭头所指的方向分别旋转
剪下图中的三角形①,②,并按图中箭头所指的方向分别旋转 .
.
(1)你能拼成一个什么样的四边形?并说明你的理由;
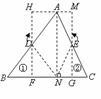 (2)请你利用这个图形,证明三角形的面积公式:
(2)请你利用这个图形,证明三角形的面积公式: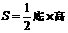 .
.
|
(1)答:拼出的四边形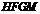 是矩形.
是矩形.
 证明:由题意,得
证明:由题意,得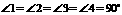
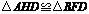
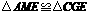
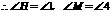
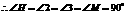
|
 四边形
四边形 是矩形.
是矩形.
(2)由题意,得
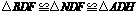

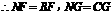 ,
,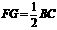
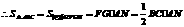
即:三角形的面积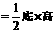 .
.
11.如图1,2所示,将一张长方形的纸片对折两次后,沿图3中的虚线 剪下,将
剪下,将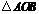 完全展开.
完全展开.
(1)画出展开图形,判断其形状,并证明你的结论;
(2)若按上述步骤操作,展开图形是正方形时,请写出 应满足的条件.
应满足的条件.
|
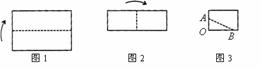
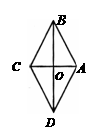 解:(1)展开图如图所示,它是菱形.(展开图只要求画出示意图即可.)
解:(1)展开图如图所示,它是菱形.(展开图只要求画出示意图即可.)
证明:由操作过程可知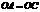 ,
, 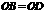 ,
, 四边形
四边形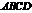 是平行四边形.又
是平行四边形.又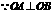 ,即
,即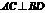 ,
, 四边形
四边形 是菱形.
是菱形.
(2) 中,
中,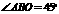 (或
(或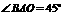 或
或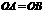 ).
).
9.如图,菱形 的对角线
的对角线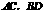 交于点
交于点 ,若
,若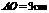 ,
,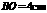 ,则菱形
,则菱形 的面积是
的面积是  .
.
|
 10.如图,将矩形纸片
10.如图,将矩形纸片 沿
沿 向上折叠,使点
向上折叠,使点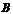 落在
落在 边上的
边上的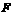 点处.若
点处.若 的周长为9,
的周长为9,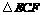 的周长为3,则矩形
的周长为3,则矩形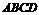 的周长为________.
的周长为________.
核心能力-----技能关