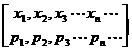0 446684 446692 446698 446702 446708 446710 446714 446720 446722 446728 446734 446738 446740 446744 446750 446752 446758 446762 446764 446768 446770 446774 446776 446778 446779 446780 446782 446783 446784 446786 446788 446792 446794 446798 446800 446804 446810 446812 446818 446822 446824 446828 446834 446840 446842 446848 446852 446854 446860 446864 446870 446878 447348
 的分布列是用表格形式给出的。教学中板书或学生作业也可写成
的分布列是用表格形式给出的。教学中板书或学生作业也可写成