摘要:已知函数(其中.为常数). 方程有两个实根,.设, 解关于的不等式. 某山区的某种特产由于运输的原因,长期只能在当地销售,当地政府对该项特产的销售投资收益为:每投入万元,可获得利润万元.当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入万元的销售投资,在未来年的前年中,每年都从万元中拨出万元用于修建一条公路,年修成,通车前该特产只能在当地销售,公路通车后的年中,该特产既在本地销售,也在外地销售,在外地销售的投资收益为:每投入万元,可获得利润万元.问从年的累积利润看,该规划方案是否可行? 如图,三棱柱的底面是边长为的等边三角形,侧面是的菱形,且平面平面,是棱上的动点. (1)当为棱的中点时,求证:, (2)试求二面角的平面角最小时三棱锥的体积. 设函数(,). (1)直线能否为函数的图象的切线?若能,求出的值,若不能,请说明理由, (2)若方程有两个不等的实根.,不等式 对于恒成立,求实数的取值范围. 反面还有试题 自然状态下的鱼类是一种可再生的资源.为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响.用表示某鱼群在第年年初的总量,,且.不考虑其他因素,设在第年内鱼群的繁殖量及被捕捞量都与成正比,死亡量与成正比,这些比例系数依次为正常数... (1)求与的关系式, (2)猜测:当且仅当...满足什么条件时,每年年初鱼群的总量保持不变(不要求证明,但要有猜测过程)? (3)设,,为保证对任意,都有(),则捕捞强度的最大允许值是多少?证明你的结论. 如图所示,且,且(),过点的任意直线(不与重合)交曲线于.两点,为的角平分线,(.),,为线段的中点. (1)建立适当的直角坐标系,求曲线的方程, (2)若,证明:, (3)若是奇素数(素数是指只能被和它自身整除的正整数),且点到直线.的距离均为非零整数,证明:到中点的距离不是整数.
网址:http://m.1010jiajiao.com/timu3_id_4468642[举报]
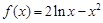
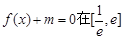 内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)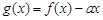 的图象与x轴交于两点
的图象与x轴交于两点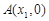 、
、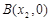 且
且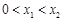 .求证:
.求证: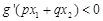 (其中正常数
(其中正常数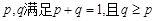 ).
).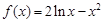
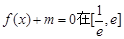 内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)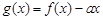 的图象与x轴交于两点
的图象与x轴交于两点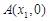 、
、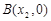 且
且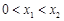 .求证:
.求证: (其中正常数
(其中正常数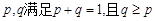 ).
).