0 138985 138993 138999 139003 139009 139011 139015 139021 139023 139029 139035 139039 139041 139045 139051 139053 139059 139063 139065 139069 139071 139075 139077 139079 139080 139081 139083 139084 139085 139087 139089 139093 139095 139099 139101 139105 139111 139113 139119 139123 139125 139129 139135 139141 139143 139149 139153 139155 139161 139165 139171 139179 447348
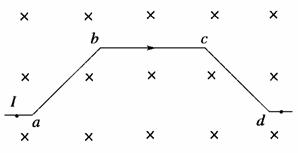
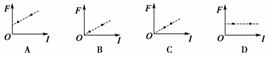

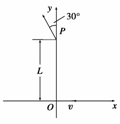
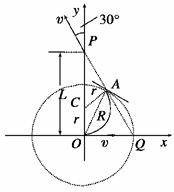
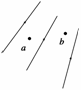 A.a、b两处的磁感应强度的大小不等Ba>Bb
A.a、b两处的磁感应强度的大小不等Ba>Bb