0 138956 138964 138970 138974 138980 138982 138986 138992 138994 139000 139006 139010 139012 139016 139022 139024 139030 139034 139036 139040 139042 139046 139048 139050 139051 139052 139054 139055 139056 139058 139060 139064 139066 139070 139072 139076 139082 139084 139090 139094 139096 139100 139106 139112 139114 139120 139124 139126 139132 139136 139142 139150 447348

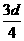 处,船的渡河速度为
处,船的渡河速度为