0 138982 138990 138996 139000 139006 139008 139012 139018 139020 139026 139032 139036 139038 139042 139048 139050 139056 139060 139062 139066 139068 139072 139074 139076 139077 139078 139080 139081 139082 139084 139086 139090 139092 139096 139098 139102 139108 139110 139116 139120 139122 139126 139132 139138 139140 139146 139150 139152 139158 139162 139168 139176 447348
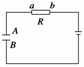 A.电阻R中没有电流
A.电阻R中没有电流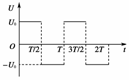
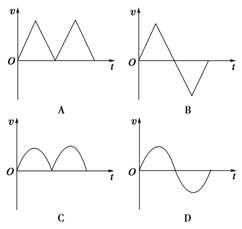
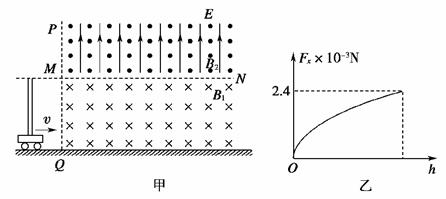

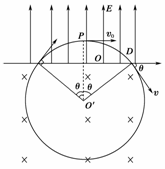 (2)垒球进入磁场时与分界面夹角为θ
(2)垒球进入磁场时与分界面夹角为θ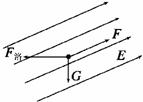
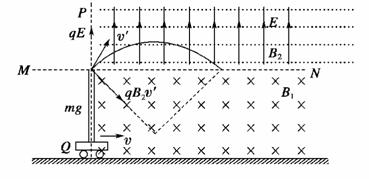
 A.该处电场方向和磁场方向重合
A.该处电场方向和磁场方向重合