苏州市2006届高三教学调研测试
数 学
注意事项:
1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页.满分150分.考试时间120分钟.
2. 请将第Ⅰ卷的答案填涂在答题卡上,第Ⅱ卷的解答写在答题卷上.在本试卷上答题无效.
第Ⅰ卷(选择题,共60分)
一、 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知全集U={a,b,c,d},集合A={a,c,d},B={b,d},则集合(CUA)∩B等于
A.{b} B.{d} C.{a,c} D.{b,d}
2.已知等差数列{an}的前n项和为Sn,若a5=18-a4,则S8等于
A.144
B
3.不等式(x-1)?|x|≥0的解集为
A.{x|x>1} B.{x|x≥1} C.{x|x>1或x=0} D.{x|x≥1或x=0}
4.若函数f(x)=x2lga-2x+1的图象与x轴有两个交点,则实数a的取值范围是
A.0<a<10 B.1<a<
5.抛物线y=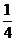 x2的焦点坐标是
x2的焦点坐标是
A.(0,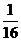 ) B.(
) B.(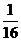 ,0)
C.(1,0)
D.(0,1)
,0)
C.(1,0)
D.(0,1)
6.设双曲线C: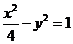 的右焦点为F,直线l过点F且斜率为k,若直线l与双曲线C的左、右两支都相交,则直线l的斜率的取值范围是
的右焦点为F,直线l过点F且斜率为k,若直线l与双曲线C的左、右两支都相交,则直线l的斜率的取值范围是
A.k≤-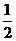 或k≥
或k≥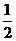 B.k<-
B.k<-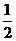 或k>
或k>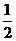
C.-
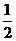 <k<
<k<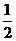 D.-
D.- 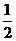 ≤k≤
≤k≤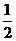
7.若一系列函数的解析式和值域相同,但定义域互不相同,则称这些函数为“同族函数”,例如函数y=x2,x∈[1,2]与函数y=x2,x∈[-2,-1]即为“同族函数”.下面4个函数中能够被用来构造“同族函数”的是
A.y=sinx B.y=x C.y=2x D.y=log2x
8.已知函数y=f(2x+1)是偶函数,则一定是函数y=f(2x)图象的对称轴的直线是
A.x=-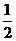 B.x=
B.x=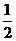 D.x=1
D.x=1
9.设m、n是不同的直线,α、β、γ是不同的平面,有以下四个命题:
①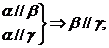 ②
②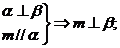 ③
③ ④
④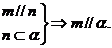
A.①② B.②③ C.①③ D.②④
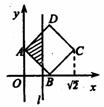 10.如图,正方形ABCD的顶点A(0,
10.如图,正方形ABCD的顶点A(0,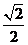 ),B(
),B(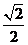 ,0),顶点C,D位于第一象限,直线l:x=t(0≤t≤
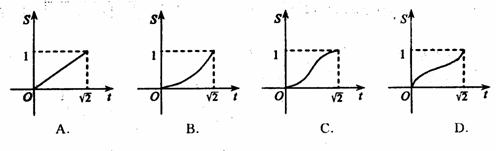
,0),顶点C,D位于第一象限,直线l:x=t(0≤t≤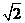 )将正方形ABCD分成两部分,记位于直线l左侧阴影部分的面积为f(t),则函数S=f(t)的图象大致是
)将正方形ABCD分成两部分,记位于直线l左侧阴影部分的面积为f(t),则函数S=f(t)的图象大致是
11.已知直线x=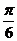 是函数y=asinx-bcosx图象的一条对称轴,则函数y=bsinx-acosx图象的一条对称轴方程是
是函数y=asinx-bcosx图象的一条对称轴,则函数y=bsinx-acosx图象的一条对称轴方程是
A.x=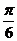 B.x=
B.x=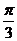 C.x=
C.x=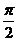 D.x=π
D.x=π
12.已知等差数列{an}的前n项和为Sn,且S2=10,S5=55,则过点P(n,an)和Q(n+2,an+2)(n∈N*)的直线的一个方向向量的坐标是
A.(2,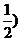 B.(-
B.(-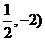 C.(-
C.(- D.(-1,-1)
D.(-1,-1)
第Ⅱ卷(非选择题,共90分)
二、 填空题:本大题共6小题,每小题4分,共24分.把答案填在答题卷相应的位置上.
13.直角坐标系xOy中,若定点A(1,2)与动点P(x,y)满足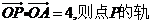

14.记地球赤道的周长为C km,则地球北纬60°的纬线圈的周长用C表示等于______km.
 15.在右侧棋子堆放的示意图中,最上层(记为第一层)有1颗棋子,第二层有3颗,第三层有6颗,…,如果按图示的方式摆放,那么堆放满5层需要的棋子总数是______颗.
15.在右侧棋子堆放的示意图中,最上层(记为第一层)有1颗棋子,第二层有3颗,第三层有6颗,…,如果按图示的方式摆放,那么堆放满5层需要的棋子总数是______颗.
16.已知椭圆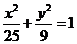 与双曲线
与双曲线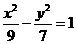 在第一象限内的交点为P,则点P到椭圆右焦点的距离等于__________.
在第一象限内的交点为P,则点P到椭圆右焦点的距离等于__________.
17.设a,b是两个不共线的向量,若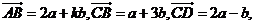 且A,B,D三点共线,则k=________.
且A,B,D三点共线,则k=________.
18.若函数f(x)=cosx+|sinx|(x∈[0,2π])的图象与直线y=k有且仅有四个不同的交点,则k的取值范围是___________.
三、解答题:本大题共5小题,共66分.请把答案写在答题卷规定的答题框内.解答应写出文字说明、证明过程或演算步骤.
19.(本小题共12分)
已知函数f(x)=-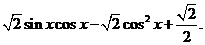
(1) 求函数y=f(x)的单调增区间;
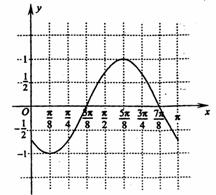
(2)  在右边的直角坐标系中画出函数y=f(x)在区间[0,π]上的图象.
在右边的直角坐标系中画出函数y=f(x)在区间[0,π]上的图象.
20.(本小题共12分)
已知函数f(x)=x+1,设g1(x)=f(x),gn(x)=f(gn-1(x)),(n>1,n∈N*).
(1) 求g2(x),g3(x)的表达式,并猜想gn(x)(n∈N*)的表达式(直接写出猜想结果)
(2)
若关于x的函数y=x2+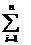 gi(x)(n∈N*)在区间(-∞,-1]上的最小值为6,求n的值.(符号“
gi(x)(n∈N*)在区间(-∞,-1]上的最小值为6,求n的值.(符号“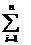 ”表示求和,例如:
”表示求和,例如: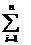 i=1+2+3+…+n.)
i=1+2+3+…+n.)
21.(本小题满分14分)
如图,梯形ABCD中,CD∥AB,AD=DC=CB=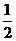 AB,E是AB中点,将△ADE沿DE折起使点A折到点P的位置,且二面角P-DE-C的大小为120°.
AB,E是AB中点,将△ADE沿DE折起使点A折到点P的位置,且二面角P-DE-C的大小为120°.
(1)
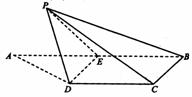 求证:DE⊥PC;
求证:DE⊥PC;
(2) 求直线PD与平面BCDE所成角的大小;
(3) 求点D到平面PBC的距离.
22.(本小题共14分)
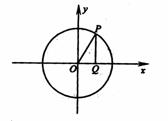 已知点P是圆x2+y2=1上的一个动点,过P作PQ⊥x轴于Q,设
已知点P是圆x2+y2=1上的一个动点,过P作PQ⊥x轴于Q,设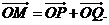
(1) 求点M的轨迹方程;
(2)
求向量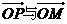 夹角的最大值,并求此时P点的坐标.
夹角的最大值,并求此时P点的坐标.
23.(本小题满分14分)
已知曲线C:y=x2(x>0),过C上的点A1(1,1)作曲线C的切线l1交x轴于点B1,再过点B1作y轴的平行线交曲线C于点A2,再过点A2作曲线C的切线l2交x轴于点B2,再过点B2作y轴的平行线交曲线C于交A3,…,依次作下去,记点An的横坐标为an(n∈N*).
(1) 求数列{an}的通项公式;
(2) 设数列{an}的前n项和为Sn,求证:anSn≤1;
(3) 求证: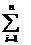
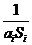 ≤
≤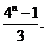
苏州市2006届高三教学调研测试
1.A 2.B 3.D 4.D 5.D 6.C 7.A 8.C 9.D 10.C 11.B 12.B
13.x+2y-4=0
14.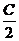 15.35 16.2 17.-8 18.1≤k≤
15.35 16.2 17.-8 18.1≤k≤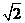
19.(1)∵f(x)=-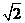 sinxcosx-
sinxcosx-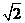 cos2x+
cos2x+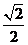
=-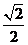 sin2x-
sin2x-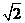 ?
?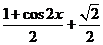
=-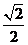 sin2x-
sin2x-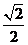 cos2x=sin(2x-
cos2x=sin(2x-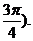
由题意,得2kπ-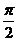 ≤2x-
≤2x-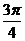 ≤2kπ+
≤2kπ+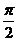 ,k∈Z.
,k∈Z.
 ∴函数y=f(x)的单调增区间为[kπ+
∴函数y=f(x)的单调增区间为[kπ+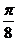 ,kπ+
,kπ+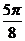 ],∈Z.
],∈Z.
(2)由y=sin(2x-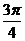 )知
)知
x
0
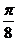
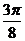
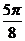
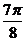
π
y
-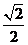
-1
0
1
0
-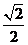
函数y=f(x)在区间[0,π]上的图象见右.
注:列出表格给3分,正确画出图象给2分.如果不列表,但图象正确,给5分.
20.(1)∵g1(x)=f(x)=x+1,
∴g2(x)=f(g1(x))=f(x+1)=(x+1)+1=x+2.
g3(x)=f(g2(x))=f(x+2)=(x+2)+1=x+3.
(2)∵gn(x)=x+n, ∴猜想gn(x)
∴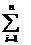 gi(x)=g1(x)+g2(x)+…+gn(x)=nx+
gi(x)=g1(x)+g2(x)+…+gn(x)=nx+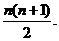
∴y=x2+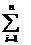 gi(x)=x2+nx+
gi(x)=x2+nx+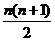 =(x+
=(x+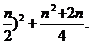
①当-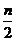 ≥-1,即n≤2时,函数y=(x+
≥-1,即n≤2时,函数y=(x+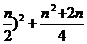 在区间(-∞,-1]上是减函数.
在区间(-∞,-1]上是减函数.
∴当x=―1时,ymin=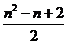 =6,即
=6,即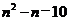 =0,该方程无整数解
=0,该方程无整数解
②当-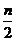 <-1,即n>2时, ymin=
<-1,即n>2时, ymin=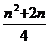 =6,解得n=4.
=6,解得n=4.
21.(1)连结AC交DE于F,连结PF.
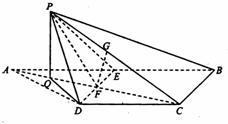 ∵CD∥AB,
∵CD∥AB,
∴∠BAC=∠ACD.
又∵AD=CD,
∴∠DAC=∠ACD.
∴∠BAC=∠DAC.
即CA平分∠BAD.
∵△ADE是正三角形,
∴AC⊥DE.
即PF⊥DE,CF⊥DE.
∴DE⊥平面PCF.
∴DE⊥PC.
(2)过P作PO⊥AC于O,连结OD.
设AD=DC=CB=a,则AB=
∵DE⊥平面PCF,∴DE⊥PO.
∴PO⊥平面BCDE.
∴∠PDO即为直线PD与平面BCDE所成的角.
∵∠PFC是二面角P-DE-C的平面角,∴∠PFO=60°
在Rt△POF中,∵∠PFO=60°,PF=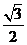 a,
a,
∴PO=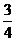 a.
a.
在Rt△POD中,sin∠PDO=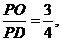
∴直线PD与平面BCDE所成角是arcsin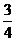 .
.
(3) ∵DE∥BC,DE在平面PBC外,
∴DE∥平面PBC.
∴点D到平面PBC的距离即为点F到平面PBC的距离.
过点F作FG⊥PC,垂足为G.
∵DE⊥平面PCF,∴BC⊥平面PCF.
∴平面PBC⊥平面PCF.
∴FG⊥平面PBC.
∴FG的长即为点F到平面PBC的距离.
在菱形ADCE中,AF=FC, ∴PF=CF=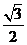 a,
a,
∵∠PFC=120°, ∴∠FPC=∠FCP=30°.
∴FG=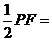
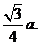
22.(1)设P(x0,y0),M(x,y),则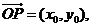
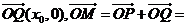 (2x0,y0)
(2x0,y0)
∴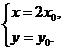 化为
化为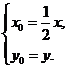 ∵x
∵x ∴
∴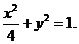
(2)设向量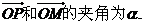
则cosα=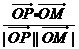
=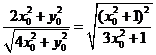
令t=3x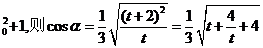 ≥
≥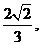
当且仅当t=2时,即P点坐标为(±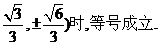
∴
23.(1)∵曲线C在点An(an,a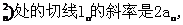
∴切线ln的方程是y-a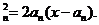
由于点Bn的横坐标等于点An+1的横坐标an+1,所以,令y=0,得an+1=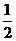 an。
an。
∴数列{an}是首项为1,公比为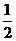 的等比数列.∴an=
的等比数列.∴an=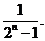
(2)∵Sn=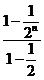 =2(1-
=2(1-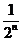 ),∴anSn=4×
),∴anSn=4×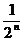 (1-
(1-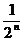 ).
).
令t=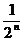 ,则0<t≤
,则0<t≤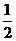 ,∴anSn=4t(1-t)=-4(t-
,∴anSn=4t(1-t)=-4(t-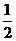 )2+1.
)2+1.
∴当t=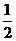 ,即n=1时,-4(t-
,即n=1时,-4(t-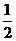 )2+1有最大值1,即anSn≤1.
)2+1有最大值1,即anSn≤1.
(3)∵Sk≥ak,k∈N*,∴akSk≥a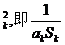 ≤
≤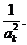
∵数列{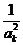 }是首项为1,公比为4的等比数列.
}是首项为1,公比为4的等比数列.
∴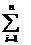
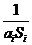 ≤
≤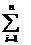
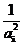 =
=