摘要：∴g2(x)=f(g1+1=x+2.
网址：http://m.1010jiajiao.com/timu_id_3805[举报]
已知f（x）=log
x，当点M（x，y）在y=f（x）的图象上运动时，点N（x-2，ny）在函数y=gn（x）的图象上运动（n∈N*）．
（1）求y=gn（x）的表达式；
（2）若方程g1（x）=g2（x-2+a）有实根，求实数a的取值范围；
（3）设Hn(x)=2gn(x)，函数F（x）=H1（x）+g1（x）（0＜a≤x≤b）的值域为[log2
，log2
]，求实数a，b的值．
查看习题详情和答案>>
| 1 |
| 2 |
（1）求y=gn（x）的表达式；
（2）若方程g1（x）=g2（x-2+a）有实根，求实数a的取值范围；
（3）设Hn(x)=2gn(x)，函数F（x）=H1（x）+g1（x）（0＜a≤x≤b）的值域为[log2
| |||
| b+2 |
| |||
| a+2 |
已知函数f（x）=x+1，设g1（x）=f（x），gn（x）=f（gn-1（x））（n＞1，n∈N*）
（1）求g2（x），g3（x）的表达式，并猜想gn（x）（n∈N*）的表达式（直接写出猜想结果）
（2）若关于x的函数y=x2+
gi(x)(n∈N*)在区间（-∞，-1]上的最小值为6，求n的值．
（符号“
”表示求和，例如：
i=1+2+3+…+n．）
查看习题详情和答案>>
（1）求g2（x），g3（x）的表达式，并猜想gn（x）（n∈N*）的表达式（直接写出猜想结果）
（2）若关于x的函数y=x2+
| n |
 |
| i=1 |
（符号“
| n |
|
| i=1 |
| n |
|
| i=1 |
已知函数f(x)=cos(x-
)．先把y=f（x）的图象上所有点向左平移
个单位长度，再把所得图象上所有点的横坐标缩短到原来的
（纵坐标不变）得到函数y=g（x）的图象．
（1）写出函数g（x）的解析式；
（2）已知f(α)=
，α∈(
，
)，求f（2α）的值；
（3）设g1（x），g2（x）是定义域为R的两个函数，满足g2（x）=g1（x+θ），其中θ是常数，且θ∈[0，π]．请设计一个函数y=g1（x），给出一个相应的θ值，使得g（x）=g1（x）•g2（x）．并予以证明．
查看习题详情和答案>>
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
（1）写出函数g（x）的解析式；
（2）已知f(α)=
| 3 |
| 5 |
| π |
| 2 |
| 3π |
| 2 |
（3）设g1（x），g2（x）是定义域为R的两个函数，满足g2（x）=g1（x+θ），其中θ是常数，且θ∈[0，π]．请设计一个函数y=g1（x），给出一个相应的θ值，使得g（x）=g1（x）•g2（x）．并予以证明．
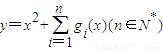在区间（-∞，-1]上的最小值为6，求n的值．
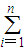”表示求和，例如：
．）
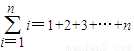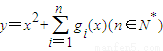在区间（-∞，-1]上的最小值为6，求n的值．
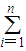”表示求和，例如：
．）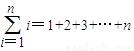