摘要:(1)∵曲线C在点An(an,a
网址:http://m.1010jiajiao.com/timu_id_3828[举报]
设曲线C:f(x)=lnx-ex(e=2.71828…),f′(x)表示f(x)导函数.
(Ⅰ)求函数f(x)的极值;
(Ⅱ)数列{an}满足a1=e,an+1=2f′(
)+3e.求证:数列{an}中不存在成等差数列的三项;
(Ⅲ)对于曲线C上的不同两点A(x1,y1),B(x2,y2),x1<x2,求证:存在唯一的x0∈(x1,x2),使直线AB的斜率等于f′(x0). 查看习题详情和答案>>
(Ⅰ)求函数f(x)的极值;
(Ⅱ)数列{an}满足a1=e,an+1=2f′(
| 1 | an |
(Ⅲ)对于曲线C上的不同两点A(x1,y1),B(x2,y2),x1<x2,求证:存在唯一的x0∈(x1,x2),使直线AB的斜率等于f′(x0). 查看习题详情和答案>>
曲线C1,C2都是以原点O为对称中心、离心率相等的椭圆.点M的坐标是(0,1),线段MN是C1的短轴,是C2的长轴.直线l:y=m(0<m<1)与C1交于A,D两点(A在D的左侧),与C2交于B,C两点(B在C的左侧).
(Ⅰ)当m=
,|AC|=
时,求椭圆C1,C2的方程;
(Ⅱ)若OB∥AN,求离心率e的取值范围.
查看习题详情和答案>>
(Ⅰ)当m=
| ||
| 2 |
| 5 |
| 4 |
(Ⅱ)若OB∥AN,求离心率e的取值范围.
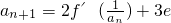 .求证:数列{an}中不存在成等差数列的三项;
.求证:数列{an}中不存在成等差数列的三项; ,
,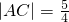 时,求椭圆C1,C2的方程;
时,求椭圆C1,C2的方程;