11.预测题
(1).(2008广东)已知两不等的实数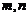 满足
满足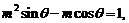
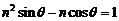 则过点
则过点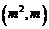 和
和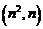 的直线与单位圆的位置关系为(
)
的直线与单位圆的位置关系为(
)
A.相切 B.相离 C.相交 D.不确定
分析:本题给出的是两个方程,所研究的是直线与圆的位置关系,,需要两点确定的直线方程,通过观察就可以把已知的方程转化为所求直线的方程,从而判断直线与圆的位置关系.
解:因为 实数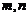 满足
满足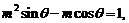
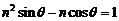 ,所以点
,所以点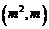 和
和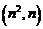 的坐标都适合直线
的坐标都适合直线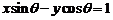 ,即两点确定的直线方程为
,即两点确定的直线方程为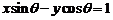 ,原点到此直线的距离为
,原点到此直线的距离为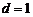 ,所以直线与圆相切.故选A
,所以直线与圆相切.故选A
答案:A
评注:不要直接由两点式写方程,要注意观察并把已知条件转化,减少计算量.
(2).(08届莆田四中)已知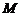 是
是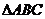 内一点,且
内一点,且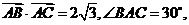 若
若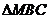 、
、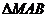 、
、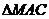 的面积分别为
的面积分别为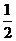 、
、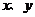 , 则
, 则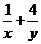 的最小值是( )
的最小值是( )
A.9 B. 16 C. 18 D. 20
分析:已知条件为向量的数量积与夹角,可以得到两边之积,再由两边与夹角求得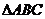 的面积,另一方面,
的面积,另一方面, 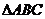 的面积又为
的面积又为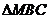 、
、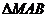 、
、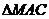 的面积之和
的面积之和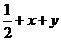 ,从而实现了由向量向代数式的转化.然后用均值不等式求得最值.
,从而实现了由向量向代数式的转化.然后用均值不等式求得最值.
解:∵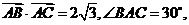 ∴
∴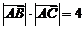 ,∴
,∴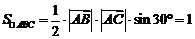 ,又因为
,又因为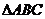 的面积为
的面积为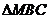 、
、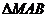 、
、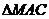 的面积之和
的面积之和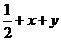 ,∴得
,∴得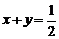
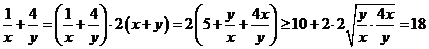 当且仅当
当且仅当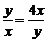 时取等号.故选C.
时取等号.故选C.
答案:C
评注:本题完成了由向量向函数方程之间的转化,进而又转化为用均值不等式求最值.做题时要注意条件的联系性和化归的数学思想.
(3)(宁夏银川一中)
|
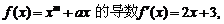
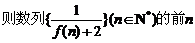 项和是
项和是
|
A.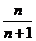 B.
B.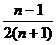 C.
C.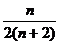 D.
D.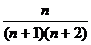
分析:把题目中的函数求出,得到解析式,从而转化为数列的通项与前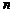 项的和.
项的和.
解: 由函数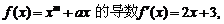 知
知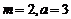 ,所以
,所以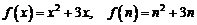 , 所以
, 所以
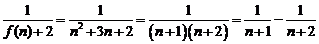 ,
,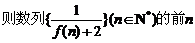 项和为
项和为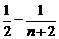 =
=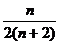 ,故选C.
,故选C.
答案:C
评注:本题中给出的已知
条件是函数与导函数,由导函数确定原函数,从而求得数列的通项公式,然后求出前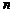 项的和.
项的和.
(4)(江苏省盐城中学)求直线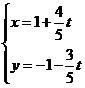 (
(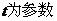 )被曲线
)被曲线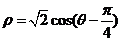 所截的弦长.
所截的弦长.
分析:本题给出的是参数方程和极坐标方程,要求弦长,就要转化为普通方程.
解:将方程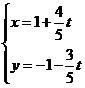 ,
,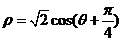 分别化为普通方程:
分别化为普通方程: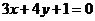 ,
,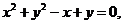
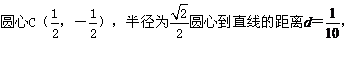
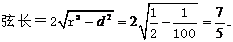
评注:对于参数方程和极坐标方程的方程,可以直接求解,也可以转化为普通方程求解出.
(5).(原创)设函数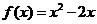 ,若
,若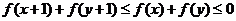 ,则点
,则点 所形成的区域的面积为 ( )
所形成的区域的面积为 ( )
A.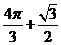 B.
B. 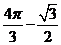 C.
C. 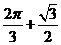 D.
D. 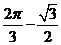
分析:首先分析由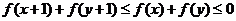 所确定的平面区域,再根据区域的形状求其面积.
所确定的平面区域,再根据区域的形状求其面积.
解:由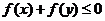 ,得
,得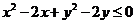 ,即
,即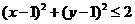 ,所表示的区域为以
,所表示的区域为以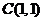 为圆心,以
为圆心,以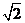 为半径的圆面.由
为半径的圆面.由 ,
,
得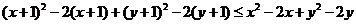 ,即
,即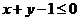 ,所表示的区域为直线
,所表示的区域为直线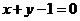 的左下方.故点
的左下方.故点 所形成的区域如图阴影部分所示.
所形成的区域如图阴影部分所示.
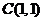 到直线
到直线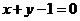 的距离为
的距离为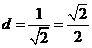 ,又
,又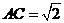 ,故
,故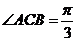 ,
,
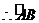 ,对应的圆心角角为
,对应的圆心角角为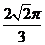 ,扇形ABC的面积为
,扇形ABC的面积为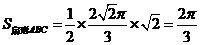 ;
;
又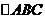 的面积为
的面积为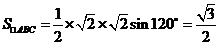 ,故阴影部分的面积为
,故阴影部分的面积为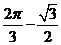 .即点
.即点 所形成的区域的面积为
所形成的区域的面积为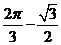 .选D.
.选D.


评注:考查圆的标准方程,点到直线的距离,一元二次方程表示平面区域,扇形的面积以及函数的表示等知识.考查运算能力和化归思想.函数,不等式的内容都是比较容易与其它知识相结合的知识点,本题在形式上是函数和不等式问题,但剖析之后可以发现,其实质是圆与线性规划相结合的问题.高考中,知识的交汇试题是主流,很多题目都是以一个知识点为载体考查另一个知识点,解题时一定要善于分析,透过表面看透问题的实质,从而合理转化,寻求问题的解决途径.
(6).(原创)已知过点(0,3)的直线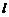 与函数
与函数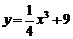 的导函数的图象交于
的导函数的图象交于 两点, ,且
两点, ,且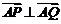 ,其中
,其中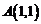
(1)求直线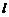 的方程,并求
的方程,并求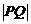 的长.
的长.
(2)问若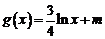 ,问实数m取何值时,使得
,问实数m取何值时,使得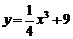 的图象恒在
的图象恒在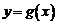 的图象的上方?
的图象的上方?
分析:根据求导公式,将函数问题转化为抛物线与直线的位置关系问题,通过解方程组,由韦达定理和向量的数量积坐标运算,利用待定系数法求解.
 解: 函数
解: 函数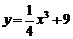 的导函数为
的导函数为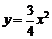 ,其图象为开口向上的抛物线, 因为直线
,其图象为开口向上的抛物线, 因为直线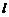 过点(0,3), 与抛物线交于
过点(0,3), 与抛物线交于 两点,所以直线
两点,所以直线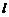 的斜率存在,设为
的斜率存在,设为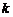 ,则直线
,则直线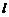 的方程为
的方程为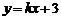 ,解方程组
,解方程组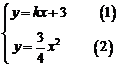 消去
消去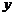 得:
得: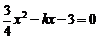 ,△
,△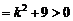 ,方程组有两解,设
,方程组有两解,设 ,则
,则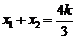 ,
,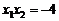 ,∴
,∴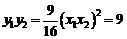 ,
,
∵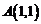 ,∴
,∴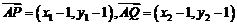 ,
,
又∵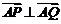 ∴
∴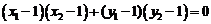 ,
,
即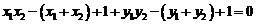 ,∴
,∴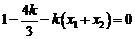 ,
,
即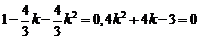 ∴
∴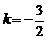 或
或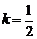 ,
,
①当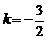 时,直线
时,直线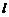 的方程为
的方程为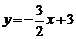 ,
,
此时,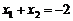 ,
,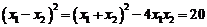 ,
,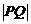 =
=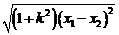 =
=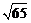 .
.
②当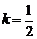 时,直线
时,直线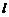 的方程为
的方程为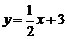 ,此时,
,此时,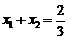 ,
,
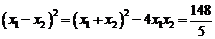 ,
,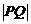 =
=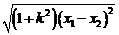 =
=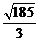 .
.
(2)设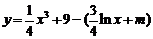 ,定义域为
,定义域为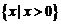
则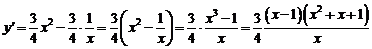 ,令
,令 ,得
,得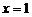 ,
,
∴当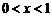 时,
时,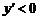 ,
,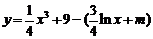 为减函数;
为减函数;
当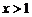 时,
时,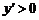 ,
,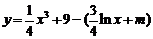 为增函数;∴当
为增函数;∴当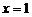 时,
时,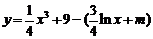 最小,最小值为
最小,最小值为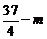 ,∴要使得
,∴要使得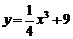 的图象恒在
的图象恒在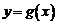 的图象的上方,需使最小值
的图象的上方,需使最小值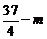 >0,即
>0,即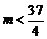
评注:考查函数求导,利用导数求函数的最值, 向量的数量积, 考查直线与圆锥曲线的位置关系等基础知识,考查利用韦达定理计算弦长等综合运算求解能力.本题通过函数求导,把问题转化为研究直线与圆锥曲线的位置关系,并把两曲线的位置关系的讨论转化为利用导数研究函数的最值的综合性题目.做题时要仔细审题,逐步翻译,求解直线或圆锥曲线的方程时往往要先设后求,利用待定系数法和解方程组法由韦达定理解答.在解答问题时要注意直线的斜率是否存在,解方程组时,判别式是否大于0,函数的定义域等这些细节问题.
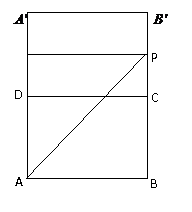
 最短路程为展开图中的线段
最短路程为展开图中的线段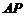 ,则
,则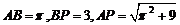
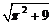
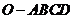 中,
中,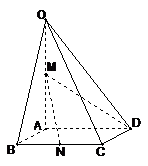 底面
底面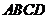 四边长为1的菱形,
四边长为1的菱形,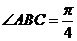 ,
, 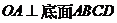 ,
, 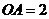 ,
,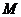 为
为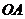 的中点,
的中点,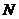 为
为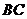 的中点
的中点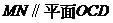
 ;
;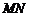 的平行线,取
的平行线,取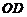 的中点,通过线线平行证出,也可以找平面的平行平面通过面面平行证出; 异面直线AB与MD所成角可以通过平移转化为平面角求出;而(Ⅲ)中点B到平面OCD的距离不易找出,可以利用线
的中点,通过线线平行证出,也可以找平面的平行平面通过面面平行证出; 异面直线AB与MD所成角可以通过平移转化为平面角求出;而(Ⅲ)中点B到平面OCD的距离不易找出,可以利用线 转化为点A到平面OCD的距离求出.还可以用向量法通过计算解答各题.
转化为点A到平面OCD的距离求出.还可以用向量法通过计算解答各题.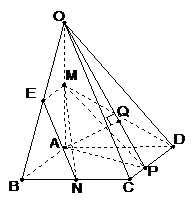 解法一:(综合法) (1)取OB中点E,连接ME,NE
解法一:(综合法) (1)取OB中点E,连接ME,NE
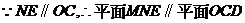
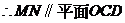
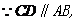
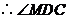 为异面直线
为异面直线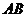 与
与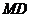 所成的角(或其补角)
所成的角(或其补角)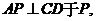 连接
连接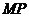
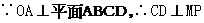
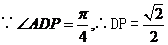
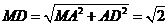
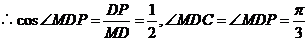 所以
所以 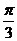
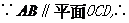 点A和点B到平面OCD的距离相等,连接OP,过点A作
点A和点B到平面OCD的距离相等,连接OP,过点A作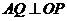 于点Q,
于点Q,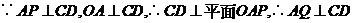
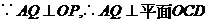 ,线段AQ的长就是点A到平面OCD的距离
,线段AQ的长就是点A到平面OCD的距离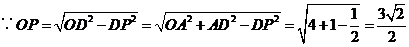 ,
,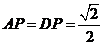
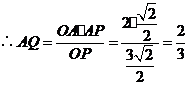 ,所以点B到平面OCD的距离为
,所以点B到平面OCD的距离为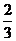
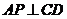 于点P,如图,分别以AB,AP,AO所在直线为
于点P,如图,分别以AB,AP,AO所在直线为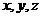 轴建立坐标系
轴建立坐标系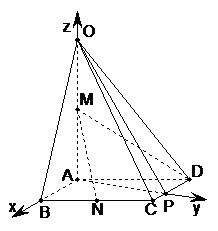
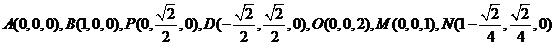 (1)
(1)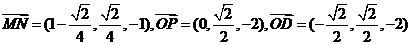
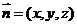 ,则
,则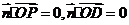
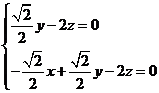 取
取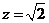 ,解得
,解得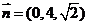
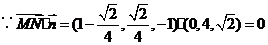
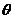 ,
,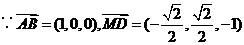
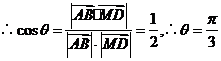 ,
, 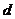 ,则
,则 在向量
在向量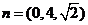 上的投影的绝对值,
上的投影的绝对值,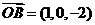 , 得
, 得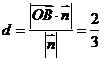 .所以点B到平面OCD的距离为
.所以点B到平面OCD的距离为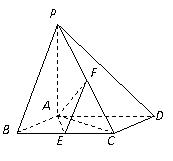 例19.(2008山东卷,理20)如图,已知四棱锥
例19.(2008山东卷,理20)如图,已知四棱锥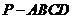 ,底面
,底面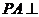 平面
平面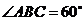 ,
,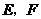 分别是
分别是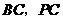 的中点.
的中点.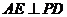 ;
;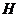 为
为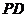 上的动点,
上的动点, 与平面
与平面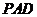 所成
所成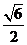 ,求二面角
,求二面角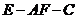 的余弦值.
的余弦值.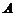 点到
点到 的距离最短,然后求出确定位置.另外,对于点的位置不确定而且比较容易建立直角坐标系时,用坐标计算比较简单。
的距离最短,然后求出确定位置.另外,对于点的位置不确定而且比较容易建立直角坐标系时,用坐标计算比较简单。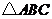 为正三角形.
为正三角形.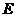 为
为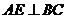 .又
.又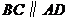 ,因此
,因此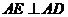 .
. 因为
因为 平面
平面 .
. 平面
平面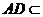 平面
平面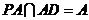 ,
,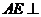 平面
平面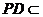 平面
平面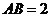 ,
,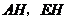 .
.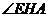 为
为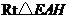 中,
中,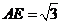 ,所以当
,所以当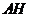 最短时,
最短时,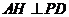 时,
时,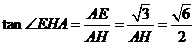 ,
,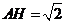 .又
.又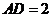 ,所以
,所以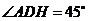 ,所以
,所以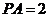 .
.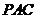 ,所以平面
,所以平面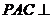 平面
平面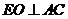 于
于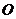 ,则
,则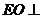 平面
平面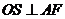 于
于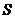 ,连接
,连接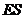 ,则
,则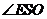 为二面角
为二面角 中,
中,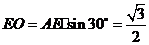 ,
,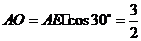 ,又
,又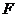 是
是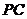 的中点,在
的中点,在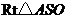 中,
中,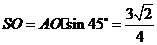 ,
,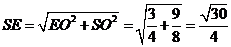 ,在
,在 中,
中,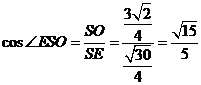 ,即所求二面角的余弦值为
,即所求二面角的余弦值为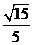 .
.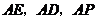 两两垂直,以
两两垂直,以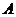 为坐标原点,建立如图所示的空间直角坐标系,又
为坐标原点,建立如图所示的空间直角坐标系,又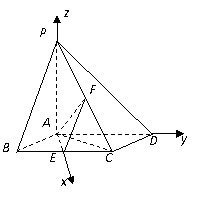
 ,
,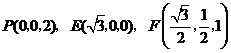 ,所以
,所以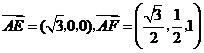 .
.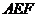 的一法向量为
的一法向量为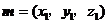 ,
,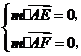 因此
因此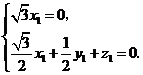
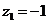 ,则
,则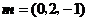 ,因为
,因为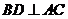 ,
,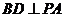 ,
,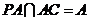 ,
,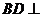 平面
平面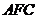 ,故
,故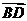 为平面
为平面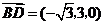 ,
,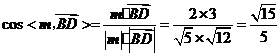 .因为二面角
.因为二面角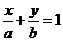 通过点
通过点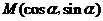 ,则( )
,则( )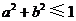 B.
B.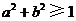 C.
C.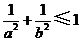 D.
D.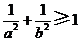
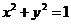 有交点,则
有交点,则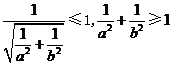 .
. ,由题意知
,由题意知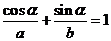
 可得
可得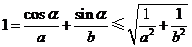
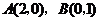 是它的两个顶点,直线
是它的两个顶点,直线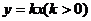 与AB相交于点D,与椭圆相交于E、F两点.
与AB相交于点D,与椭圆相交于E、F两点.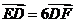 ,求
,求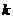 的值;
的值;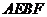 面积的最大值.
面积的最大值.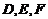 都在直线
都在直线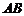 为公共边,也可以以
为公共边,也可以以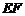 为公共边求出。
为公共边求出。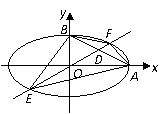 (Ⅰ)解:依题设得椭圆的方程为
(Ⅰ)解:依题设得椭圆的方程为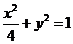 ,
,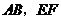 的方程分别为
的方程分别为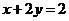 ,
,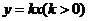 .
.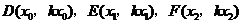 ,其中
,其中 ,
,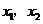 满足方程
满足方程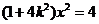 ,故
,故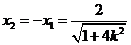 .①
.①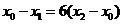 ,得
,得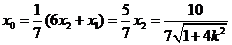 ;
;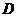 在
在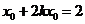 ,得
,得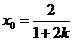 .所以
.所以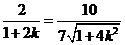 ,
,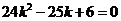 ,解得
,解得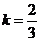 或
或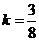 .
.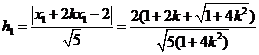 ,
,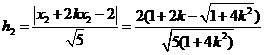 .
.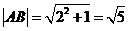 ,所以四边形
,所以四边形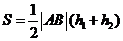
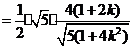
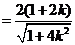
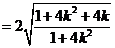
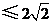 ,
,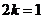 ,即当
,即当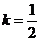 时,上式取等号.所以
时,上式取等号.所以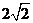 .
.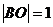 ,
,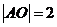 .设
.设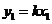 ,
,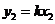 ,由①得
,由①得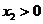 ,
,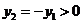 ,
,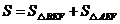
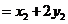
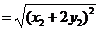
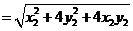
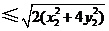
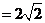 ,
,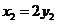 时,上式取等号.所以
时,上式取等号.所以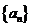 满足
满足 ,则称数列
,则称数列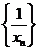 为调和数列,且
为调和数列,且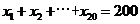 ,则
,则 。
。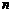 项和。
项和。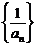 为等差数列,现在数列
为等差数列,现在数列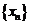 为等差数列,那么由
为等差数列,那么由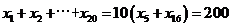 ,
,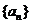 的首项
的首项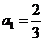 ,
,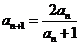 ,
,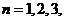 ….
….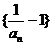 是等比数列;(Ⅱ)数列
是等比数列;(Ⅱ)数列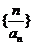 的前
的前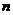 项和
项和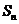 .
.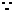
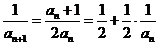 ,
,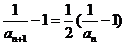 ,又
,又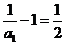 ,
,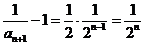 ,即
,即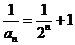 ,
,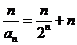 .
.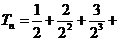 …
… , ①
, ①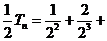 …
…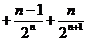 ,②
,②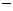 ②得
②得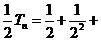 …
…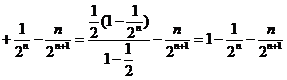 ,
,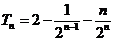 .又
.又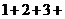 …
…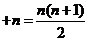 .
.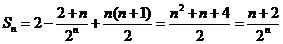
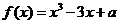 有三个不同的零点,则实数
有三个不同的零点,则实数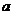 的取值范围是
的取值范围是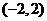 B.
B.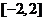 C.
C.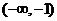 D.
D.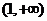
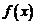 有两个极值点,且有
有两个极值点,且有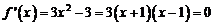 ,得
,得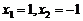 ,所以函数
,所以函数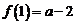 和
和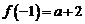 ,结合图象,应该有
,结合图象,应该有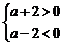 ∴
∴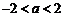 ,故选A
,故选A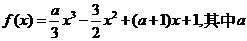 为实数。
为实数。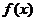 在
在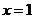 处取得极值,求
处取得极值,求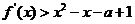 对任意
对任意 都成立,求实数
都成立,求实数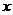 的取值范围。
的取值范围。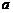 的不等式在
的不等式在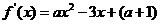 ,由于函数
,由于函数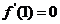
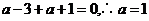
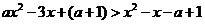 对任意
对任意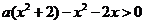 对任意
对任意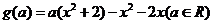 , 则对任意
, 则对任意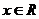 ,
,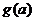 为单调递增函数
为单调递增函数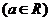
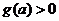 恒成立的充分必要条件是
恒成立的充分必要条件是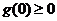
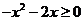 ,
,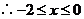 , 于是
, 于是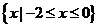
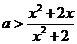 对任意
对任意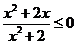
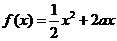 ,
,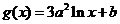 ,其中
,其中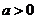 .设两曲线
.设两曲线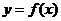 ,
,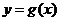 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.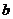 ,并求
,并求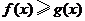 (
(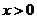 ).
). 在公共点
在公共点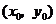 处的切线相同.
处的切线相同.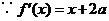 ,
,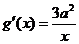 ,由题意
,由题意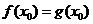 ,
,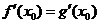 .
. 由
由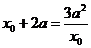 得:
得: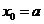 ,或
,或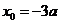 (舍去).
(舍去).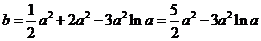 .
.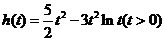 ,则
,则 .于是
.于是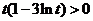 ,即
,即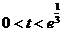 时,
时,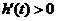 ;
;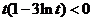 ,即
,即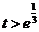 时,
时,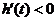 .
.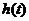 在
在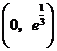 为增函数,在
为增函数,在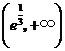 为减函数,
为减函数,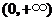 的最大值为
的最大值为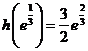 .
.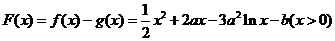 ,
,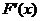
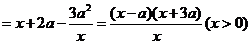 .
.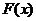 在
在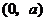 为减函数,在
为减函数,在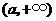 为增函数,
为增函数,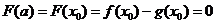 .
.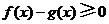 ,即当
,即当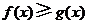 .
.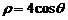 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: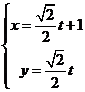 ,求直线l与曲线C相交所成的弦的弦长.
,求直线l与曲线C相交所成的弦的弦长.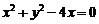 ,即
,即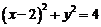 直线l的参数方程
直线l的参数方程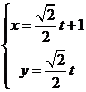 ,化为普通方程为x-y-1=0,
,化为普通方程为x-y-1=0,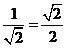
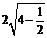 =
=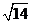 .
. 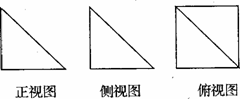 例8.(2009莱阳模拟)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形.若该几何体的体积为V,并且可以用n这样的几何体拼成一个棱长为4的正方体,则V,n的值是(
)
例8.(2009莱阳模拟)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形.若该几何体的体积为V,并且可以用n这样的几何体拼成一个棱长为4的正方体,则V,n的值是(
)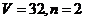 B.
B.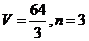
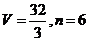 D.
D.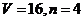
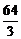 ,故选B
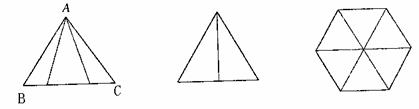
,故选B 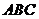 是边长为
是边长为 的正三角形,俯视图为正六边形,那么该几何体的侧视图的面积为(
)
的正三角形,俯视图为正六边形,那么该几何体的侧视图的面积为(
) 
 正视图
侧视图
俯视图
正视图
侧视图
俯视图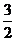 B.
B.
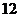 D.
D.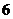
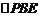 ,是正三角形,则
,是正三角形,则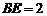 ,∴底面边长为1,侧棱长为2,
,∴底面边长为1,侧棱长为2, ,设
,设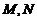 分别为
分别为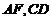 的中点,则
的中点,则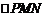 为侧视图,
为侧视图,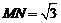 ,∴侧视图的面积为
,∴侧视图的面积为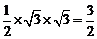 ,故选
,故选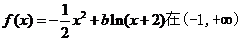 上是减函数,则
上是减函数,则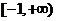 B.
B. 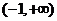 C.
C. 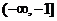 D.
D. 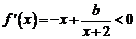 在
在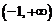 上恒成立,即
上恒成立,即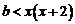 在
在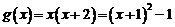 在
在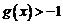 ,∴当
,∴当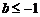 时,
时,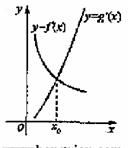
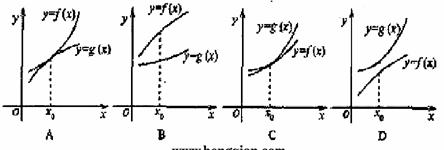
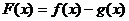 ,则
,则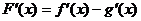 ,当
,当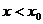 时,由图象知
时,由图象知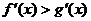 ,即
,即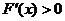 ,
,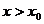 时,
时,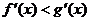 ,即
,即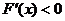 ,
,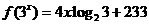 ,
,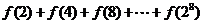 的值等于
.
的值等于
.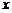 为整体,而是以
为整体,而是以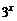 为整体给出的解析式,所以要求函数值,需要先求关于
为整体给出的解析式,所以要求函数值,需要先求关于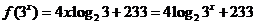 ,∴
,∴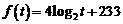 ,
,
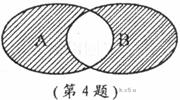 例3.(2008山东省泰安市)如图所示的韦恩图中,A、B是非空集合,定义集合A#B为阴影部分表示的集合.若
例3.(2008山东省泰安市)如图所示的韦恩图中,A、B是非空集合,定义集合A#B为阴影部分表示的集合.若 ,
,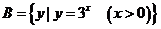 ,
则A#B为(
)
,
则A#B为(
)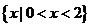 B.
B.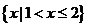
 D.
D.
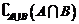 ,所以需要求出
,所以需要求出 和
和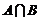 ,借助数轴求出并集与交集。
,借助数轴求出并集与交集。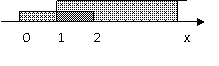 解:
解: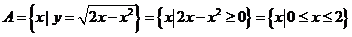 ,
,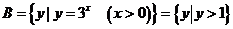 ,则
,则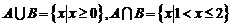 ,根据新运算,得A#B=
,根据新运算,得A#B=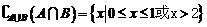 故选D
故选D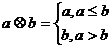 ,令
,令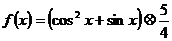 ,且
,且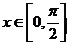 ,则函数
,则函数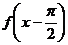 的最大值是( )
的最大值是( ) B.1 C.
B.1 C.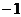 D.
D.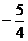
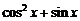 与
与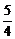 的大小关系,即需要求
的大小关系,即需要求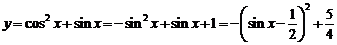 ,
,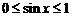 ,∴
,∴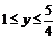 ,即
,即 ,
,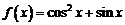 ,
,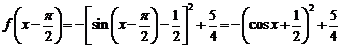 (
(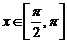 )
)