摘要:7.函数.方程.不等式之间的转化 例11.若函数有三个不同的零点.则实数的取值范围是 A. B. C. D. 分析:本题为三次函数有三个不同的零点.则函数应该有两个极值点.一个极值为正.一个极值为负.所以要先求出其导数.再求其极值. 解: 由函数有三个不同的零点,则函数有两个极值点,且有,得,所以函数的两个极值为和,结合图象,应该有∴,故选A 答案:A 评注:一般地对于高次函数来说.要转化为导函数研究问题.特别是在研究函数的单调性.最值等性质时要用导数解决. 例12.设函数为实数. (Ⅰ)已知函数在处取得极值.求的值, (Ⅱ)已知不等式对任意都成立.求实数的取值范围. 分析:(Ⅱ)中不等式对任意都成立.可以转化为的不等式在都成立.从而变为的一次函数由单调性来解答,也可以将分化出来.转化为的不等式在恒成立.研究右边函数的最值. 解: (1).由于函数在时取得极值.所以 即 (2) 方法一: 由题设知:对任意都成立 即对任意都成立 设 , 则对任意.为单调递增函数 所以对任意.恒成立的充分必要条件是 即 .. 于是的取值范围是 方法二:由题设知:对任意都成立 即对任意都成立 于是对任意都成立.即 . 于是的取值范围是 评注:对于不等式恒成立问题.一般来说是要分化出参数.转化为求右边函数的最值问题,但有的也不容易分化.我们也可以转换主变量.把二次函数转化为一次函数.根据一次函数的单调性即可容易完成. 已知定义在正实数集上的函数..其中.设两曲线.有公共点.且在该点处的切线相同. (I)用表示.并求的最大值, (II)求证:(). 本小题主要考查函数.不等式和导数的应用等知识.考查综合运用数学知识解决问题的能力. 解:(Ⅰ)设与在公共点处的切线相同. ..由题意.. 即由得:.或. 即有. 令.则.于是 当.即时., 当.即时.. 故在为增函数.在为减函数. 于是在的最大值为. (Ⅱ)设. 则. 故在为减函数.在为增函数. 于是函数在上的最小值是. 故当时.有.即当时..
网址:http://m.1010jiajiao.com/timu_id_3980696[举报]
已知函数f(x)=x2+bx+c(b,c∈R),并设F(x)=
,
(1)若F(x)图象在x=0处的切线方程为x-y=0,求b、c的值;
(2)若函数F(x)是(-∞,+∞)上单调递减,则
①当x≥0时,试判断f(x)与(x+c)2的大小关系,并证明之;
②对满足题设条件的任意b、c,不等式f(c)-Mc2≤f(b)-Mb2恒成立,求M的取值范围.
查看习题详情和答案>>
| f(x) | ex |
(1)若F(x)图象在x=0处的切线方程为x-y=0,求b、c的值;
(2)若函数F(x)是(-∞,+∞)上单调递减,则
①当x≥0时,试判断f(x)与(x+c)2的大小关系,并证明之;
②对满足题设条件的任意b、c,不等式f(c)-Mc2≤f(b)-Mb2恒成立,求M的取值范围.
 请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.
请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.(1)选修4-1:几何证明选讲
如图,在△ABC中,D是AC的中点,E是BD的中点,AE的延长线交BC于F.
(Ⅰ)求
| BF |
| FC |
(Ⅱ)若△BEF的面积为S1,四边形CDEF的面积为S2,求S1:S2的值.
(2)选修4-4:坐标系与参数方程
以直角坐标系的原点O为极点,a=
| π |
| 6 |
| π |
| 6 |
( I)写出直线l的参数方程;
( II)设l与圆ρ=2相交于两点A、B,求点P到A、B两点的距离之积.
(3)选修4-5:不等式选讲
已知函数f(x)=|2x+1|+|2x-3|.
(I)求不等式f(x)≤6的解集;
(II)若关于x的不等式f(x)>a恒成立,求实数a的取值范围. 查看习题详情和答案>>
.(本小题满分16分)
已知函数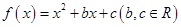 ,并设
,并设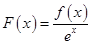 ,
,
(1)若 图像在
图像在 处的切线方程为
处的切线方程为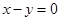 ,求
,求 、
、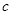 的值;
的值;
(2)若函数 是
是 上单调递减,则
上单调递减,则
① 当 时,试判断
时,试判断 与
与 的大小关系,并证明之;
的大小关系,并证明之;
② 对满足题设条件的任意 、
、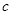 ,不等式
,不等式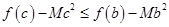 恒成立,求
恒成立,求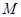 的取值范围
的取值范围
查看习题详情和答案>>
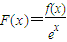 ,
, 求证:(1)
求证:(1)