7. 预测题
预测题
(1)(2008宁夏银川一中,改编)已知函数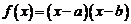 (其中
(其中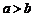 ),
),


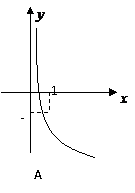 若
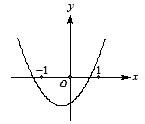
若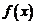 的图像如右图所示,则函数
的图像如右图所示,则函数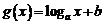 的图像是( )
的图像是( )

分析:由已知二次函数解析式及二次函数的图象可以判断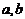 的取值范围,从而判断
的取值范围,从而判断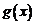 的图象.
的图象.
解: 由函数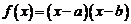 (其中
(其中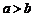 )的图象可知,
)的图象可知,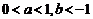 .把
.把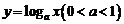 的图象向下平移
的图象向下平移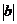 个单位,故选A.
个单位,故选A.
答案:A
评注:学会识图,读图,画图,并进行图象的平移变换.
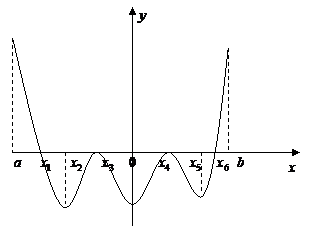 (2)(2008山东省聊城市,改编)函数
(2)(2008山东省聊城市,改编)函数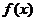 的定义域为(a,b),其导函数
的定义域为(a,b),其导函数
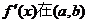 内的图象如图所示,则函
内的图象如图所示,则函
数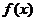 在区间(a,b)内极值点的个数是 ( )
在区间(a,b)内极值点的个数是 ( )
A.1 B.2 C.3 D. 4
分析:要判断函数的极值点,要先找导函数的零点,再看此点
两侧的导函数的符号,如果异号就是原函数的极值点.
解:由导函数图知, 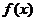 只在
只在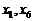 处的导数值为0,且两侧的符号相异.
处的导数值为0,且两侧的符号相异.
函数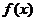 在区间(a,b)内极值点的个数为2个
在区间(a,b)内极值点的个数为2个
评注:判断函数的极值点不能只找导函数的零点,还要看此零点两侧的导函数的符号,如果异号就是原函数的极值点.本题图中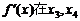 处虽然也为零,但因其两侧的符号相同,而不是函数
处虽然也为零,但因其两侧的符号相同,而不是函数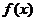 在区间(a,b)内极值点.
在区间(a,b)内极值点.
(3)(原创)设实数x, y满足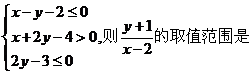
 分析: 作出不等式表示的可行域,再画出可行域内的点与点
分析: 作出不等式表示的可行域,再画出可行域内的点与点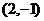 连线,数形结合解答.
连线,数形结合解答.
解: 作出不等式表示的可行域如图所示,
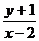 表示可行域内的点与点
表示可行域内的点与点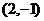 连线的斜率,
连线的斜率,
则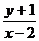 的取值范围是
的取值范围是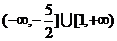
答案: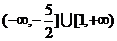
评注:作出不等式表示的可行域后, 在画出可行域内的点与
点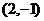 连线时,要画准确,其中有一条直线的斜率不存在,
连线时,要画准确,其中有一条直线的斜率不存在,
注意斜率的取值范围应该为两直线对应的斜率之外.
(4)(08山东卷,理12改编)设二元一次不等式组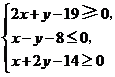 所表示的平面区域为
所表示的平面区域为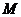 ,使函数
,使函数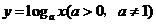 的图象过区域
的图象过区域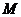 的
的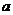 的取值范围是( )
的取值范围是( )
A.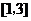 B.
B.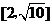 C.
C.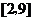 D.
D.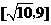
分析:先画出不等式表示的平面区域,再画出对数函数的图象,借助图形解答。
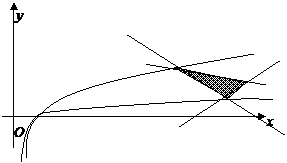 解:
区域
解:
区域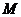 是一个三角形区域,三个顶
是一个三角形区域,三个顶
点的坐标是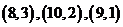 ,结合图
,结合图
形检验可知当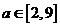 时,符合题目要求。
时,符合题目要求。
评注:解决不等式表示的平面区域和
函数问题都要用数形结合,做到一目了然。
(5)(2008海南卷,理11,改编)已知点P在抛物线 上,那么点P到点
上,那么点P到点 的距离与点P到
的距离与点P到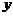 轴的距离之和取得最小值时,点P的坐标为( )
轴的距离之和取得最小值时,点P的坐标为( )
A. B.
B.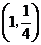 C.
C.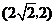 D.
D.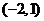
分析: 点P到点 的距离与点P到
的距离与点P到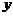 轴的距离之和取得最小值时, 点P到点
轴的距离之和取得最小值时, 点P到点 的距离与点P到抛物线的准线的距离之和也取得最小值,这样就可以把点P到抛物线的准线的距离转为到焦点的距离求出.
的距离与点P到抛物线的准线的距离之和也取得最小值,这样就可以把点P到抛物线的准线的距离转为到焦点的距离求出.
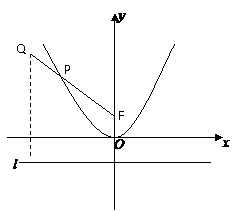 解: 点
解: 点 在抛物线
在抛物线 的外部,要使点P到点
的外部,要使点P到点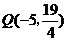 的距离与点P到
的距离与点P到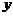 轴的距离之和取得最小值,根据抛物线的定义知,须使点P到点
轴的距离之和取得最小值,根据抛物线的定义知,须使点P到点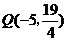 的距离与点P到抛物线焦点距离之和取得最小,即
的距离与点P到抛物线焦点距离之和取得最小,即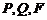 三点共线时最小. 由斜率
三点共线时最小. 由斜率
公式得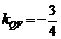 ,所以
,所以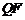 的方程为
的方程为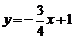 ,
,
解方程组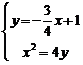 得,点
得,点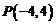 ,故选A.
,故选A.
答案:A
评注:抛物线的定义是到焦点的距离等于到准线的距离,
做题时常常用定义进行转化.
(6)、已知函数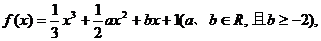 当
当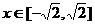 时,总有
时,总有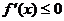 .
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设函数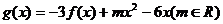 ,求证:当
,求证:当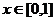 时,
时,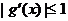 的充要条件是
的充要条件是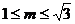 .
.
分析:三次函数的导函数为二次函数,那么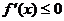 为二次不等式,当
为二次不等式,当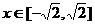 时,总有
时,总有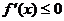 .就要结合二次函数的图象进行转化;当
.就要结合二次函数的图象进行转化;当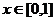 时,
时,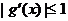 成立也是二次不等式恒成立问题也要结合着二次函数的图象完成。
成立也是二次不等式恒成立问题也要结合着二次函数的图象完成。
解:(Ⅰ)由条件,得 ,
,
当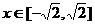 时,总有
时,总有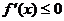 ,所以有
,所以有
|
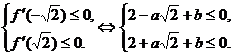
由①+②得,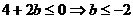 ,
,
又b≥-2,∴b=-2,把b=-2代入①和②得
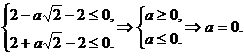
因此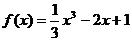 .
.
(Ⅱ) ,
,
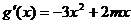 是关于x的二次函数,
是关于x的二次函数,
当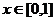 时,
时, 或
或
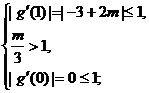 或
或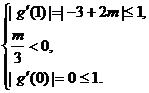
解得,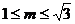 . 因此,当
. 因此,当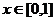 时,
时,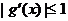 的充要条件是
的充要条件是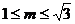
评注:二次函数,二次方程,二次不等式问题常常要结合着二次函数的图象来完成,对于二次不等式来说一般要从二次抛物线的开口方向,对称轴,判别式和端点对应的函数值四方面来解答。

 在中,
在中, ,
,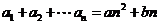 ,
,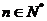 ,其中
,其中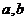 为常数,则
为常数,则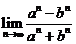 的值是 .
的值是 .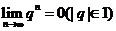 )来解决新的极限问题.
)来解决新的极限问题.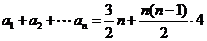
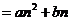 ,解得
,解得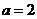 ,
,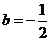 ,从而
,从而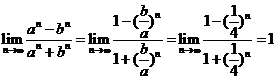 .
.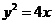 上,那么点P到点
上,那么点P到点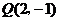 的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( ) A.
A.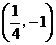 B.
B.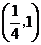 C.
C.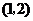 D.
D.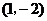
 距离与点P到抛物线焦点的距离之和取得最小值,根据抛物线的
距离与点P到抛物线焦点的距离之和取得最小值,根据抛物线的 时最小.则
时最小.则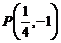 故选A.
故选A.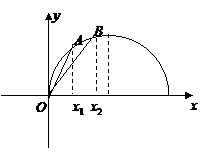 解:由函数
解:由函数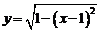 得
得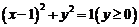 知
知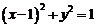 的上半圆,如图,当0<x1<x2<1时,和分别
的上半圆,如图,当0<x1<x2<1时,和分别 的斜率,由图可知
的斜率,由图可知 ,∴ > ,故选A
,∴ > ,故选A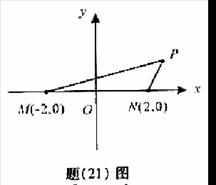 例12.(2008重庆卷,理21)如图(21)图,M(-2,0)和N(2,0)是平面上的两点,动点P满足:
例12.(2008重庆卷,理21)如图(21)图,M(-2,0)和N(2,0)是平面上的两点,动点P满足: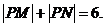
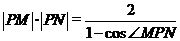 ,求点P的坐标.
,求点P的坐标.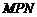 中研究边与角之间的关系。
中研究边与角之间的关系。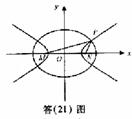 因此半焦距c=2,长半轴a=3,从而短半轴,b=
因此半焦距c=2,长半轴a=3,从而短半轴,b=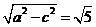 ,
,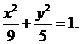
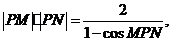 得
得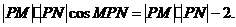 ①
①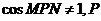 不为椭圆长轴顶点,故P、M、N构成三角形.在△PMN中,
不为椭圆长轴顶点,故P、M、N构成三角形.在△PMN中,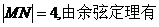
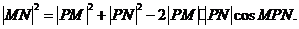 ②
②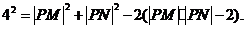 故点P在以M、N为焦点,实轴长为
故点P在以M、N为焦点,实轴长为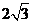 的双曲线
的双曲线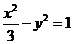 上. 由(Ⅰ)知,点P的坐标又满足
上. 由(Ⅰ)知,点P的坐标又满足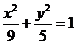 ,所以由方程组
,所以由方程组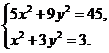 解得
解得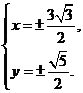 即P点坐标为
即P点坐标为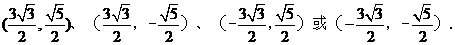
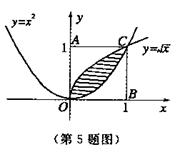 ).曲线
).曲线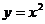 和
和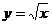 围成一个叶形图(如图所示阴影部分),
围成一个叶形图(如图所示阴影部分),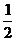 C.
C.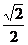 D.
D.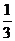
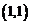 ,阴影部分的面积为
,阴影部分的面积为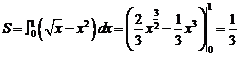
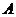 为不等式组
为不等式组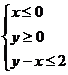 表示的平面区域,
表示的平面区域,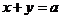 扫过
扫过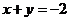 和
和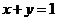
 是斜边为3 的等腰直角三角形,
是斜边为3 的等腰直角三角形, 是直
是直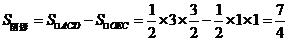
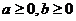 ,且当
,且当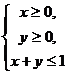 时,恒有
时,恒有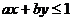 ,则以
,则以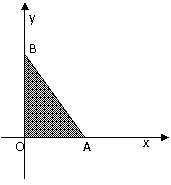 分析:本小题主要考查线性规划的相关知识,可考虑特殊情形,
分析:本小题主要考查线性规划的相关知识,可考虑特殊情形,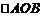 ,如图,
,如图,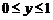
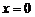 时,
时,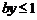 恒成立,当
恒成立,当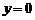 成立;当
成立;当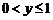 时,
时,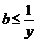 恒成立,∴
恒成立,∴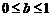 ;同理,
;同理,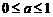 ∴以
∴以