0 49917 49925 49931 49935 49941 49943 49947 49953 49955 49961 49967 49971 49973 49977 49983 49985 49991 49995 49997 50001 50003 50007 50009 50011 50012 50013 50015 50016 50017 50019 50021 50025 50027 50031 50033 50037 50043 50045 50051 50055 50057 50061 50067 50073 50075 50081 50085 50087 50093 50097 50103 50111 447348
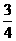 B.
B.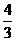 C.
C.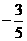 D.
D.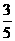
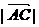 =5,
=5,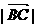 =3,
=3,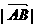 =6,则
=6,则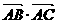 =( )
=( )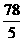 D.24
D.24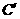 处,这时异面直线AD与
处,这时异面直线AD与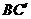 所成角的余弦值是( )
所成角的余弦值是( )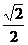 B.
B.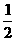 C.
C.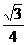 D.
D.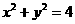 没有交点,则过(m,n)的直线与椭圆
没有交点,则过(m,n)的直线与椭圆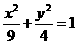 的交点个数( )
的交点个数( )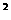 -4|b|
-4|b|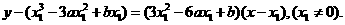
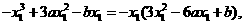
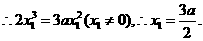 4分
4分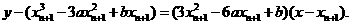
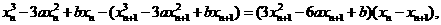
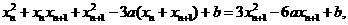
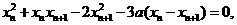 以x n-xn+1除之,得x n+2xn+1-3a=0.
9分
以x n-xn+1除之,得x n+2xn+1-3a=0.
9分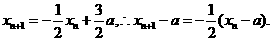
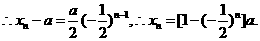
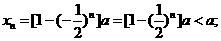
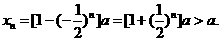 14分
14分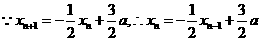 =
=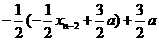
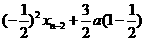 ==
==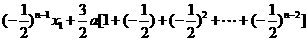 =
=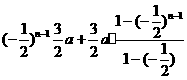 =
=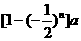 .以下同解法1.
.以下同解法1.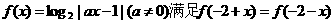 ,则实数a值是( )
,则实数a值是( )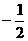 C.
C.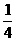 D.-1
D.-1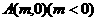 作一直线
作一直线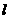 交抛物线C:
交抛物线C: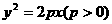 于P、Q两点,又Q关于x轴对称点为Q1,连结PQ1交x轴于B点.
于P、Q两点,又Q关于x轴对称点为Q1,连结PQ1交x轴于B点.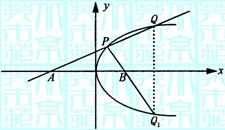 (1)求证:直线PQ1恒过一定点;
(1)求证:直线PQ1恒过一定点;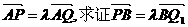 .
.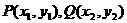 ,而Q1与Q关于x轴对称,则
,而Q1与Q关于x轴对称,则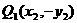 PQ直线方
PQ直线方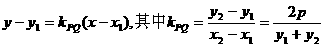
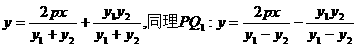
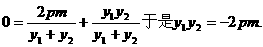
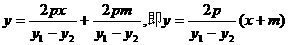
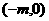 ……………………(8分)
……………………(8分)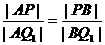
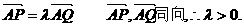
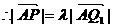 于是
于是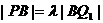
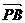 、
、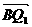 同向,
同向,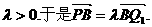 ………(14分)
………(14分)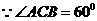 )
) tan ∠PDE = =
tan ∠PDE = =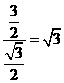 ,
,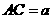 则
则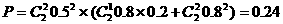 ……6分
……6分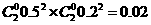
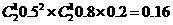
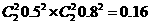
 ∴
∴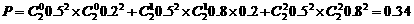 13分
13分