摘要:如图1.将三角板放在正方形ABCD上.使三角板的直角顶点E与正方形ABCD的顶点A重合.三角扳的一边交CD于点F.另一边交CB的延长线于点G. (1)求证:EF=EG, (2)如图2.移动三角板.使顶点E始终在正方形ABCD的对角线AC上.其他条件不变.(1)中的结论是否仍然成立?若成立.请给予证明:若不成立.请说明理由: 中的“正方形ABCD 改为“矩形ABCD .且使三角板的一边经过点B.其他条件不变.若AB=a.BC=b.求的值. 考点:相似三角形的判定与性质,全等三角形的判定与性质,矩形的性质,正方形的性质. 分析:(1)由∠GEB+∠BEF=90°.∠DEF+∠BEF=90°.可得∠DEF=∠GEB.又由正方形的性质.可利用SAS证得Rt△FED≌Rt△GEB.则问题得证, (2)首先点E分别作BC.CD的垂线.垂足分别为H.I.然后利用SAS证得Rt△FEI≌Rt△GEH.则问题得证, (3)首先过点E分别作BC.CD的垂线.垂足分别为M.N.易证得EM∥AB.EN∥AD.则可证得△CEN∽△CAD.△CEM∽△CAB.又由有两角对应相等的三角形相似.证得△GME∽△FNE.根据相似三角形的对应边成比例.即可求得答案. 解答:(1)证明:∵∠GEB+∠BEF=90°.∠DEF+∠BEF=90°. ∴∠DEF=∠GEB. 又∵ED=BE. ∴Rt△FED≌Rt△GEB. ∴EF=EG, (2)成立. 证明:如图.过点E分别作BC.CD的垂线.垂足分别为H.I. 则EH=EI.∠HEI=90°. ∵∠GEH+∠HEF=90°.∠IEF+∠HEF=90°. ∴∠IEF=∠GEH. ∴Rt△FEI≌Rt△GEH. ∴EF=EG, (3)解:如图.过点E分别作BC.CD的垂线.垂足分别为M.N. 则∠MEN=90°. ∴EM∥AB.EN∥AD. ∴△CEN∽△CAD.△CEM∽△CAB. ∴.. ∴.即=. ∵∠IEF+∠FEM=∠GEM+∠FEM=90°. ∴∠GEM=∠FEN. ∵∠GME=∠FNE=90°. ∴△GME∽△FNE. ∴. ∴. 点评:此题考查了正方形.矩形的性质.以及全等三角形与相似三角形的判定与性质.此题综合性较强.注意数形结合思想的应用.
网址:http://m.1010jiajiao.com/timu3_id_496985[举报]
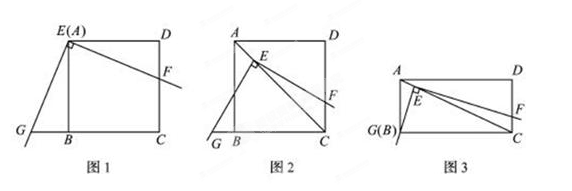
如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F.另一边交CB的延长线于点G.
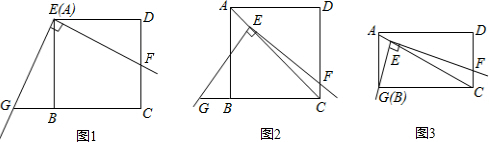
(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求
的值.
查看习题详情和答案>>

(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求
| EF | EG |
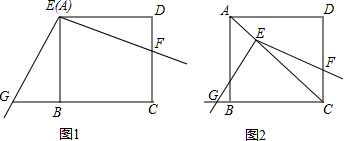
如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角板的一边交CD于点F,另一边交CB的延长线于点G.
(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变.(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
查看习题详情和答案>>
(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变.(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.

(2011•临沂)如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角扳的一边交CD于点F.另一边交CB的延长线于点G.

(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求 的值.
查看习题详情和答案>>
的值.
查看习题详情和答案>>

(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求
 的值.
查看习题详情和答案>>
的值.
查看习题详情和答案>>
 将三角板放在正方形
将三角板放在正方形 上,使三角板的直角顶点
上,使三角板的直角顶点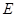 与正方形
与正方形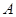 重合,三角扳的一边交
重合,三角扳的一边交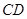 于点
于点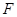 .另一边交
.另一边交 的延长线于点
的延长线于点 .
.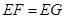 ;
;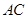 上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理
上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理 由:
由: ,其他条件不变,若
,其他条件不变,若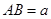 、
、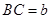 ,求
,求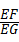 的值.
的值.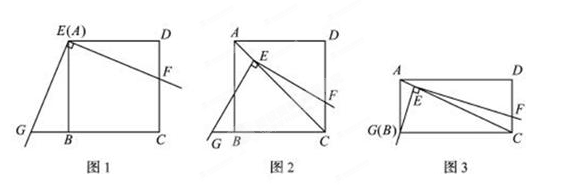
 将三角板放在正方形
将三角板放在正方形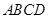 上,使三角板的直角顶点
上,使三角板的直角顶点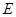 与正方形
与正方形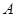 重合,三角扳的一边交
重合,三角扳的一边交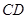 于点
于点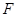 .另一边交
.另一边交 的延长线于点
的延长线于点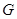 .
. ;
;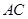 上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理
上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理 由:
由: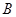 ,其他条件不变,若
,其他条件不变,若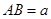 、
、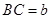 ,求
,求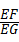 的值.
的值.