21.(2010年江苏省泰州市济川实验初中中考模拟题)小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)实验.
(1)他们在一次实验中共掷骰子60次,试验的结果如下:
|
朝上的点数 |
1 |
2 |
3 |
4 |
5 |
6 |
|
出现的次数 |
7 |
9 |
6 |
8 |
20 |
10 |
①填空:此次实验中“5点朝上”的频率为___________;
②小红说:“根据实验,出现5点朝上的概率最大.”她的说法正确吗?为什么?
(2)小颖和小红在实验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率
最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
答案:(1)①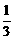 ,
,
②小红的说法是错误的. 在这次试验中,“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大.因为当试验的次数较大时,频率稳定于概率,但并不完全等于概率.
(2 )图略,点数之和为7的概率最大, P(点数之和为7)=
)图略,点数之和为7的概率最大, P(点数之和为7)=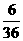 =
=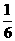 .
.
17.(2010年河南中考模拟题3)水果种植大户小方,为了吸引更多的顾客,组织了观光采摘游活动,每一位来摘水果的顾客都有一次抽奖机会:在一只不透明的盒子里有A、B、C、D四张外形完全相同的卡片,抽奖时先随机抽出一张卡片,再从盒子中剩下的3张中随机抽取第二张。
(1)请利用树状图(或列表)的方法,表示前后两次抽得的卡片所有可能的情况。
(2)如果抽得的两张卡片是同一种水果图片就可获得奖励,那么得到奖励的概率是多少?
答案:列表如下:
|
|
A |
B |
C |
D |
|
A |
|
(A,B) |
(A,C) |
(A,D) |
|
B |
(B,A) |
|
(B,C) |
(B,D) |
|
C |
(C,A) |
(C,B) |
|
(C,D) |
|
D |
(D,A) |
(D,B) |
(D,C) |
|
获奖的概率P=4/12=1/3
16.(2010年河南中考模拟题2)将背面完全相同,正面上分别写有数字1、2、3、4的四张卡片混合后,小明从中随机抽取一张,把卡片上的数字作为被减数。将形状大小完全相同,分别标有数字1、2、3的三个小球混合后,小华从中随机抽取一个,把小球上的数字作为减数,然后 计算出这两数的差。
计算出这两数的差。
(1)请你用画树状图或列表的方法,求这两数的差为0的概率。
(2)小明与小华做游戏,规则是:若这两数的差为负数,则小明胜,否则,小华胜。你认为该游戏公平吗?请说明理由。如果不公平,请你修改规则,使游戏公平。
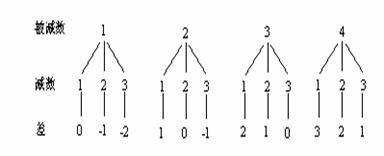
 答案:(1)其树状图如下:
答案:(1)其树状图如下:
|
|
1 |
2 |
3 |
4 |
|
1 |
0 |
1 |
2 |
3 |
|
2 |
-1 |
0 |
1 |
2 |
|
3 |
-2 |
-1 |
0 |
1 |
由图表知所有可能结果有12种,其中差为0 的有3种,所以这两数差为0 的概率P=1/4
(2)不公平
理由如下:由(1)知所有可能结果有12种,这两数差为非负数的有9种其概率为P1=3/4,这两数的差为负数的概率为P2=1/4,因为3/4≠1/4,所以,该游戏不公平,游戏规则修改为:若两数的差为正数,则小明赢;否则,小华赢。
15.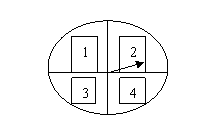 (2010年河南中考模拟题1)有一个可以自由转动的转盘,
(2010年河南中考模拟题1)有一个可以自由转动的转盘,
被分成了4个相同的扇形,分别标有数1、2、3、4(如图所
示)另一个不透明的口袋装有分别标有数0、1、3的三个小球
(出数不同外,其余都相同)。小亮转动一次转盘,停止后指
针指向木一扇形,扇形内的数是小亮的幸运数,小红任意摸出一个小球,小球上的数是小红的吉祥数,然后计算这两个数的积
(1)请你用画树状图或列表的方法,求这两个数的积为0的概率。
(2)小亮和小红做游戏,规则是:若这两个数的积为奇数,小亮赢;否则,小红赢。你认为该游戏公平吗?为什么?如果不公平,请你修改该游戏规则,使游戏公平。
答案:解:(1)列表如下
|
|
1 |
2 |
3 |
4 |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
2 |
3 |
4 |
|
3 |
3 |
6 |
9 |
12 |
由表知,所有可能的结果有12种,其中积为零的有4种,所以极为0的概率为
P=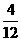 =
=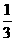 。
。
(2)不公平。由表中可知极为奇数的有4种,极为偶数的有8种。所以,即为奇数的概率为P1=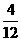 =
=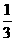 .极为偶数的概率为P2=
.极为偶数的概率为P2=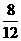 =
=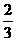 。因为
。因为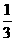 ≠
≠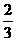 ,所以游戏不公平。
,所以游戏不公平。
游戏规则可修改为:
若这两个数的积为0,则小亮赢;极为奇数,则小红赢。(只要正确即可)
 下列运算中,错误的是( )
下列运算中,错误的是( )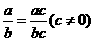 B.
B.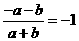
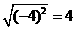 D.
D.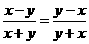
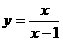 自变量的取值范围是……………… ( )
自变量的取值范围是……………… ( )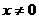 B.
B.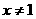 C.
C.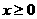 D.
D.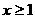
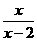 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )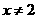 B.
B.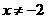 C.
C.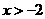 D.
D.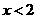
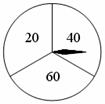 (1)列表(或画树状图)表示亮亮转出的所有可能结果.(3分)
(1)列表(或画树状图)表示亮亮转出的所有可能结果.(3分)
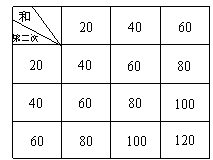 答案:(1)列表:
答案:(1)列表: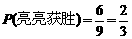 .
.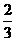 ,那么应添加多少张“太阳”卡片?请说明理由?
,那么应添加多少张“太阳”卡片?请说明理由?
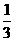 ,P(抽中小花)=
,P(抽中小花)=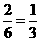 ,(3)3张。
,(3)3张。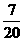
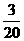
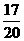 ,∴甲输而乙获胜的可能性较大.”
,∴甲输而乙获胜的可能性较大.”