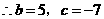10.(2010年江苏省泰州市济川实验初中中考模拟题) 某企业信息部进行市场调研发现:
信息一:如果单独投资A种产品,所获利润yA(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表:
|
x(万元) |
1 |
2 |
2.5 |
3 |
5 |
|
yA(万元) |
0.4 |
0.8 |
1 |
1.2 |
2 |
信息二:如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间存在二次函数关系:yB=ax2+bx,且投资2万元时获利润2.4万元,当投资4万元时,可获利润3.2万元.
(1)求出yB与x的函数关系式.
(2)从所学过的一次函数、二次函数、反比例函数中确定哪种函数能表示yA与x之间的关系,并求出yA与x的函数关系式.
(3)如果企业同时对A、B两种产品共投资15万元,请设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?
答案:(1)yB=-0.2x2+1.6x,
(2)一次函数,yA=0.4x,
(3)设投资B产品x万元,投资A产品(15-x)万元,投资两种产品共获利W万元, 则W=(-0.2x2+1.6x)+0.4(15-x)=-0.2x2+1.2x+6=-0.2(x-3)2+7.8,
∴当x=3时,W最大值=7.8,
答:该企业投资A产品12万元,投资B产品3万元,可获得最大利润5.8 万元.
万元.
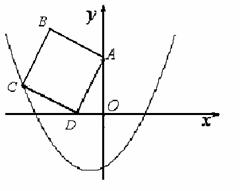 (江西南昌一模)在平面直角坐标系中,正方形ABCD纸片如图放置,A(0,2),D(-1,0),抛物线
(江西南昌一模)在平面直角坐标系中,正方形ABCD纸片如图放置,A(0,2),D(-1,0),抛物线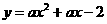 经过点C.
经过点C. 轴于T,过C作
轴于T,过C作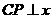 轴于P,可证得
轴于P,可证得
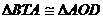 .
.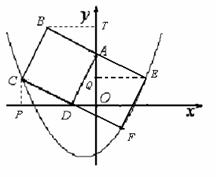 则
则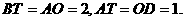
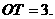
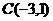
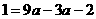 ,解得
,解得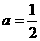 ,
,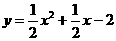 ;
; 作
作 轴于Q,作
轴于Q,作 轴于P.
轴于P. ,得
,得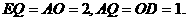
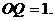 ∴E(2,1).同理F(1,-1).
∴E(2,1).同理F(1,-1).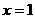 时,
时,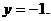 ∴F(1,-1)在抛物线上.
∴F(1,-1)在抛物线上.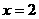 时,
时,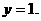 ∴E(2,1)在抛物线上.
∴E(2,1)在抛物线上.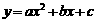 经过(-1,0),(0,-3),(2,-3)三点.
经过(-1,0),(0,-3),(2,-3)三点.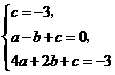 解得a=1,b=
解得a=1,b= -2,c=-3.
-2,c=-3.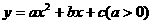 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=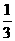 .
. 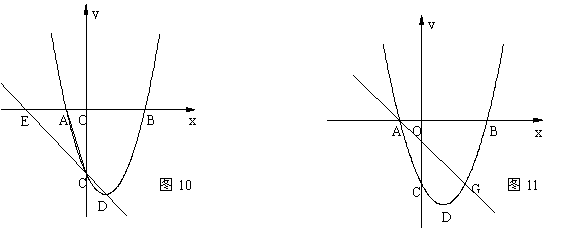
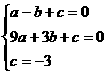
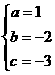
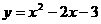
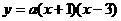
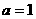
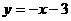
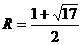
 代入抛物线的表达式,解得
代入抛物线的表达式,解得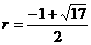
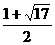 或
或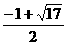 .
. 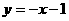 .
.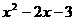 ),则Q(x,-x-1),PQ
),则Q(x,-x-1),PQ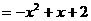 .
.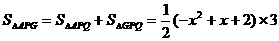
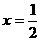 时,△APG的面积最大
时,△APG的面积最大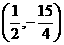 ,
, .
. 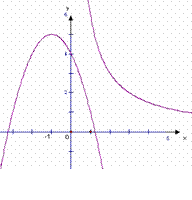 (2010 河南模拟)如图,曲线C是函数
(2010 河南模拟)如图,曲线C是函数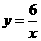 在第一现象内的图像,抛物线是函数
在第一现象内的图像,抛物线是函数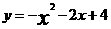 的图像,点
的图像,点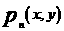 (n=1,2…)在曲线上,且x,y都是整数。
(n=1,2…)在曲线上,且x,y都是整数。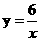 ,
,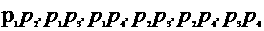 共六条;
共六条;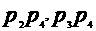 与抛物线有公共点,
与抛物线有公共点,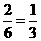 。
。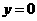 ,得
,得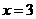 ,
, 点
点 的坐标是
的坐标是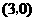
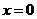 ,得
,得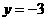 ,
, 的坐标是
的坐标是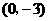
 图象如右所示。
图象如右所示。 二次函数
二次函数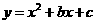 的图象经过点
的图象经过点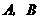 ,
,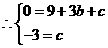 ,解得:
,解得: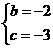 .
. 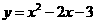 ,
, ,
, 函数
函数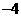 .
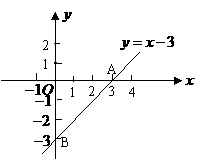
. 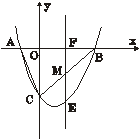 (2010福建模拟)如图,在平面直角坐标系中,直线
(2010福建模拟)如图,在平面直角坐标系中,直线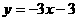 与
与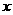 轴交于点A,与y轴交于点C. 抛物线
轴交于点A,与y轴交于点C. 抛物线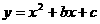 经过A、C两点,且与x轴交于另一点B(点B在点A右侧).
经过A、C两点,且与x轴交于另一点B(点B在点A右侧).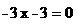
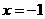 ∴A(-1, 0)
∴A(-1, 0) 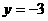 ∴ C(0,-3)
∴ C(0,-3)
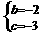 ∴
∴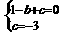 ∴
∴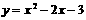 抛物线的解析式是:
抛物线的解析式是:
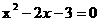 解得: x1=-1 x2=3 ∴ B(3, 0)
解得: x1=-1 x2=3 ∴ B(3, 0) 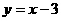
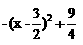
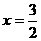 时,ME的最大值=
时,ME的最大值=

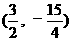 ,M
,M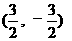
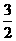 ,BF=OB-OF=
,BF=OB-OF=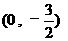 或 P2
或 P2 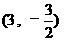
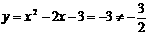 当P1
当P1 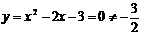 当P2
当P2 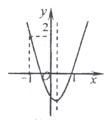 第(2)问:给出四个结论:①abc<0②2a+b>0③a+c=1④a>1.其中正确结论的序号(答对得5分,少选、错选均不得分)
第(2)问:给出四个结论:①abc<0②2a+b>0③a+c=1④a>1.其中正确结论的序号(答对得5分,少选、错选均不得分) abc>0;
abc>0;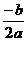
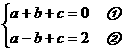 ①+②得 2a+2c=2 a+c=1 a=1-c
①+②得 2a+2c=2 a+c=1 a=1-c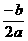 =
=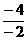 =2 k=
=2 k=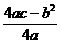 =
=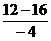
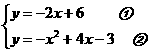
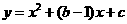 经过点
经过点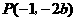 .
.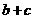 的值;
的值;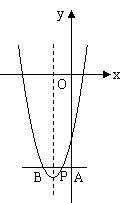 (2)若
(2)若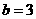 ,求这条抛物线的顶点坐标;
,求这条抛物线的顶点坐标;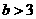 ,过点
,过点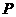 作直线
作直线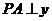 轴,交
轴,交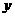 轴于点
轴于点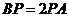 ,求这条抛物线所对应的二次函数关系式.(提示:请画示意图思考)
,求这条抛物线所对应的二次函数关系式.(提示:请画示意图思考)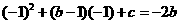 ,
,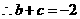 .
.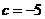 ,
,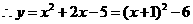
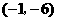 .
.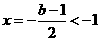 ,
,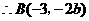
 .
.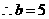 .
.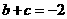 ,
,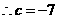 .
.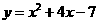 .
.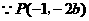 ,且
,且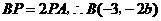
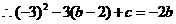 .
.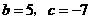
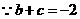 ,
,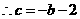 ,
,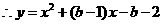 分
分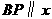 轴,
轴,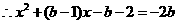
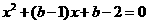 .
.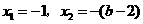 ,即
,即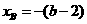
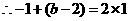 .
.