11.(2010山东新泰)小明和小刚做一个“配紫色”的游戏,用如图所示的两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色。规则如下:分别旋转两个转盘,若其中一个转盘出现了红色,另一个转盘出现了蓝色,则可配成紫色,此时小刚得1分,否则小明得1分.这个游戏对双方公平吗?请说明理由.若你认为不公平,如何修改游戏规则,才能够使游戏对双方公平?


答案:游戏对双方不公平.
游戏结果分析如下:“√”表示配成紫色,“×”表示不能够配成紫色.
|
|
红 |
蓝 |
黄 |
|
红 |
× |
√ |
× |
|
蓝 |
√ |
× |
× |
因为P(配成紫色)=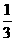 ,P(配不成紫色)=
,P(配不成紫色)=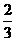 ,所以小刚得分:
,所以小刚得分: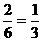 ,小明得分:
,小明得分: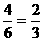 .
.
所以游戏对双方不公平.
修改规则为:若配成紫色,小刚得2分,否则小明得1分,此游戏对双方才公平 .(方法不唯一)
.(方法不唯一)
9.(2010年武汉市中考拟)武汉某中学2009年元旦晚会上,主持人安排了抽奖活动.具体方法是:设置如下表所示的翻板,每次抽奖翻开一个数字,数字背面写有所中奖品或新年祝词.
|
1 |
2 |
3 |
|
4 |
5 |
6 |
|
7 |
8 |
9 |
|
奖MP4一个 |
万事如意 |
学业进步 |
|
身体健康 |
新年快乐 |
奖MP3一个 |
|
奖笔记本一个 |
奖钢笔一支 |
心想事成 |
(1)主持人想知道“第一个人抽奖中奖”的概率,而且觉得翻版牌太麻烦,请你设计一个简便的模拟抽奖方法,并估计“第一个人抽奖中奖”的概率.
(2)若晚会开始前给每名入场的学生发一张入场券,其中有100张后标有“新年快乐”.晚会进行中主持人任意邀请台下50名同学上台合唱“同一首歌”,并宣布这50名同学的入场券后标有“新年快乐”的参与抽奖,结果有4人中奖,中奖率为40%,请估计参加本次晚会的学生人数.
答案:(1)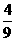 (2)500
(2)500


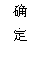

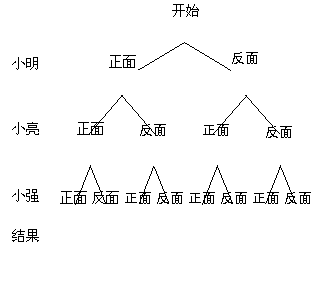
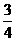 .
. 因为为了要取得最后一根,甲必须最后留下零根火柴给乙,故在最后一步之前的轮取中,甲不能留下1根或2根或3根,否则乙就可以全部取走而获胜。如果留下4根,则乙不能全取,则不管乙取几根(1或2或3),甲必能取得所有剩下的火柴而赢了游戏。同理,若桌上留有8根火柴让乙去取,则无论乙如何取,甲都可使这一次轮取後留下4根火柴,最后也一定是甲获胜。由上分析可知,甲只要使得桌面上的火柴数为4﹑8﹑12﹑16...等让乙去取,则甲必稳操胜券。因此若原先桌面上的火柴数为15,则甲应取3根。(∵15-3=12)
因为为了要取得最后一根,甲必须最后留下零根火柴给乙,故在最后一步之前的轮取中,甲不能留下1根或2根或3根,否则乙就可以全部取走而获胜。如果留下4根,则乙不能全取,则不管乙取几根(1或2或3),甲必能取得所有剩下的火柴而赢了游戏。同理,若桌上留有8根火柴让乙去取,则无论乙如何取,甲都可使这一次轮取後留下4根火柴,最后也一定是甲获胜。由上分析可知,甲只要使得桌面上的火柴数为4﹑8﹑12﹑16...等让乙去取,则甲必稳操胜券。因此若原先桌面上的火柴数为15,则甲应取3根。(∵15-3=12)
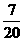
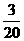
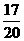 ,∴甲输而乙获胜的可能性较大.”
,∴甲输而乙获胜的可能性较大.”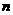 个小球,其中两个是白球,其余为红球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,从袋中随机地取出一个球,它是红球的概率是
个小球,其中两个是白球,其余为红球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,从袋中随机地取出一个球,它是红球的概率是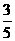 .
.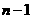 ,随机地取出一个小球后不放回,再随机地取出一个小球,求第二次取出小球标号大于第一次取出小球标号的概率。
,随机地取出一个小球后不放回,再随机地取出一个小球,求第二次取出小球标号大于第一次取出小球标号的概率。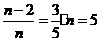 .
. 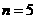 时,这5个球两个标号为1,其余标号分别为2,3,4.
时,这5个球两个标号为1,其余标号分别为2,3,4.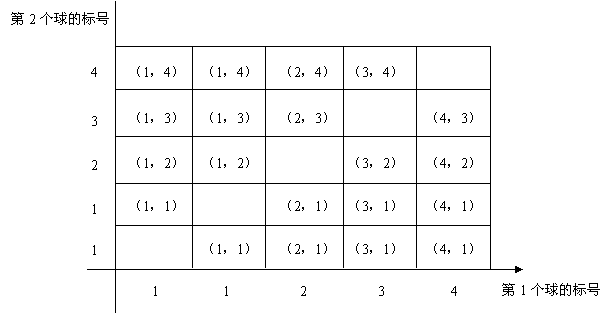
 由上表知所求概率为
由上表知所求概率为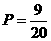 .
.  :从这两个纸箱中各随机摸出一个小球,然后把两个小球上的数字相乘,若得到的积是2的倍数,则甲得1分,若得到积是3的倍数,则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
:从这两个纸箱中各随机摸出一个小球,然后把两个小球上的数字相乘,若得到的积是2的倍数,则甲得1分,若得到积是3的倍数,则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
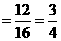
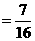
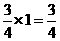 (分)
(分)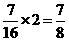 (分)
(分) 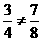
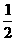 .
. 白1
白2
黄
蓝
白1
白2
黄
蓝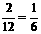 共有12种可能结果.
共有12种可能结果.