8.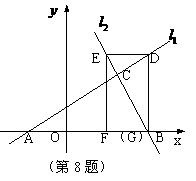 (2010浙江永嘉)如图,已知
(2010浙江永嘉)如图,已知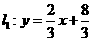 直线与直线
直线与直线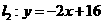 相交于点C,
相交于点C,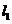 、
、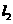 分别交
分别交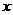 轴于A、B两点.矩形DEFG的顶点D、E分别在直线
轴于A、B两点.矩形DEFG的顶点D、E分别在直线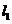 、
、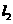 上,顶点
上,顶点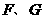 都在
都在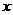 轴上,且点
轴上,且点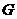 与点
与点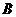 重合.
重合.
(1)求 的面积;
的面积;
(2)求矩形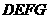 的边
的边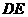 与
与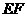 的长;
的长;
(3)若矩形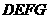 从点B出发,沿
从点B出发,沿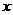 轴以每秒1个单位长度的速度向点A平移,设移动时间为
轴以每秒1个单位长度的速度向点A平移,设移动时间为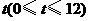 秒,矩形
秒,矩形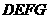 与
与 重叠部分的面积为
重叠部分的面积为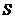 ,求
,求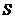 关于
关于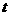 的函数关系式,并写出相应的
的函数关系式,并写出相应的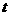 的取值范围.
的取值范围.
(1)解:∵A(-4,0) B(8,0) C(5,6)
∴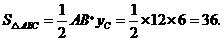
|
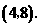
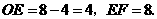
(3)解: 当
当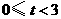 时,如图1,矩形
时,如图1,矩形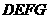 与
与 重叠部分为五边形
重叠部分为五边形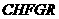
(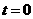 时,为四边形
时,为四边形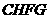 ).过
).过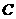 作
作 于
于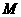 ,则
,则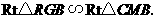

∴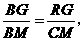 即
即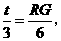 ∴
∴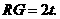
AF=8-t
∴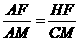
即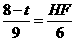
∴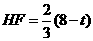
∴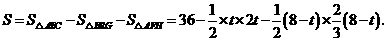
|
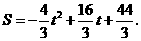
②当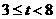 时,如图2,矩形DEFG与△ABC重叠部分为梯形QFGR(t=8时,为△ARG),则AF=8-t , AG=12-t 由Rt△AFQ∽Rt△AGR∽Rt△AMC得
时,如图2,矩形DEFG与△ABC重叠部分为梯形QFGR(t=8时,为△ARG),则AF=8-t , AG=12-t 由Rt△AFQ∽Rt△AGR∽Rt△AMC得
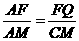 ,
,
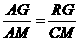 即
即 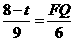 ,
,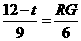
∴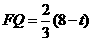 ,
, 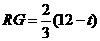
∴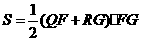 =
=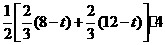 =
=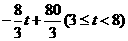
③
当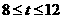 时,如图3,其重叠部分为△AGR,则AG=12-t ,
时,如图3,其重叠部分为△AGR,则AG=12-t , 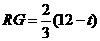
∴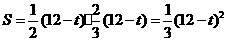
 ,图中∠MPN的度数为( )
,图中∠MPN的度数为( ) (3) 当t为何值时,△APQ的面积为
(3) 当t为何值时,△APQ的面积为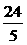 个平方单位?
个平方单位?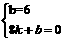 解得
解得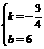
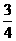 x+6.
x+6. 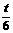 =
=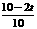 解得 t=
解得 t=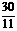 (秒)
(秒) 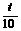 =
=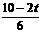 解得 t=
解得 t=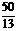 (秒)
(秒) 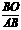 =
=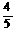
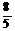 t 2分S△APQ=
t 2分S△APQ=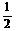 AP·QE=
AP·QE=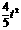 +4t=
+4t=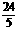 解得t=2(秒)或t=3(秒).
解得t=2(秒)或t=3(秒). 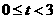 )
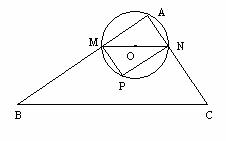
) (黑龙江一模)如图,∠ABM为直角,点C为线段BA的中点,
(黑龙江一模)如图,∠ABM为直角,点C为线段BA的中点, DA,并说明理由.
DA,并说明理由. 中,
中,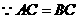 ,
,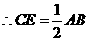 ,
,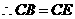 ,
,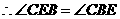 .
.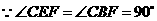 ,
,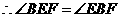 ,
,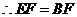 .
.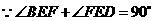 ,
,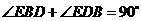 ,
,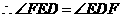 .
.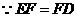 .
.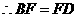 .(2)由(1)
.(2)由(1)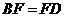 ,而
,而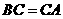 ,
,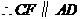 ,即
,即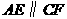 .
.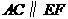 ,则
,则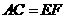 ,
,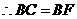 .
.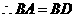 ,
,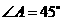 .
. 当
当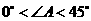 或
或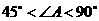 时,四边形
时,四边形 为梯形.
为梯形.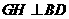 ,垂足为
,垂足为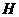 ,则
,则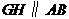 .
.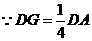 ,
,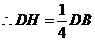 .
. 为
为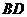 中点,
中点,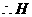 为
为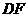 的中点.
的中点.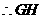 为
为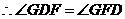 .
. 点
点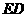 h上,
h上,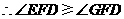 .
.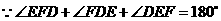 ,
,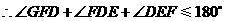 .
.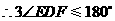 .
.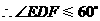 .
.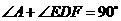 ,
,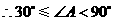 .
.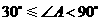 时,
时,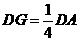 .
. ∵OA=6,OC=8,∴AC=10
∵OA=6,OC=8,∴AC=10 (3) 当t为何值时,△APQ的面积为
(3) 当t为何值时,△APQ的面积为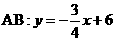 ;
;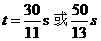 ;
; (3)
(3)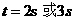 .
. ,动点M,N分别从点O,B同时出发,以每秒1个单位的速度运动,其中点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NPBC,交AC于点P,连结MP,当两动点运动了t秒时。
,动点M,N分别从点O,B同时出发,以每秒1个单位的速度运动,其中点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NPBC,交AC于点P,连结MP,当两动点运动了t秒时。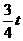 )(用含t的代数式表示)。
)(用含t的代数式表示)。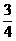 t
t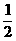 MA·PD=
MA·PD=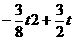 (0<t<4)
(0<t<4) =
=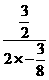 =2s S有最大值, S最大=
=2s S有最大值, S最大= (平方单位)
(平方单位)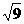 m=0,m2=6
m=0,m2=6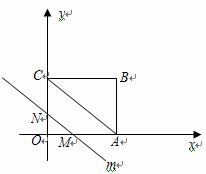 (2010年河南中考模拟题4)如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O
(2010年河南中考模拟题4)如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O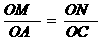 ,
,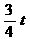 ,S=
,S=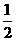 ×OM×ON=
×OM×ON=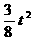 .
. 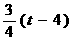 .
.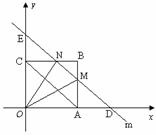 而△OND的高是3.
而△OND的高是3.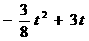 .
. 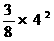 =6;
=6; 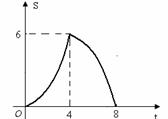 综上,当t=4时,S有最大值6.
综上,当t=4时,S有最大值6. 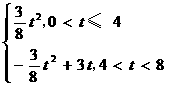
 (2010年河南中考模拟题3)在△ABC中,∠A=9
(2010年河南中考模拟题3)在△ABC中,∠A=9 0°,AB=4,AC=3,M是AB上的动点(不与A、B重合),过点M作MN∥BC交AC于点N. 以MN为直径作⊙O,并在⊙O内作内接矩形AMPN,令AM=x.
0°,AB=4,AC=3,M是AB上的动点(不与A、B重合),过点M作MN∥BC交AC于点N. 以MN为直径作⊙O,并在⊙O内作内接矩形AMPN,令AM=x. MN
MN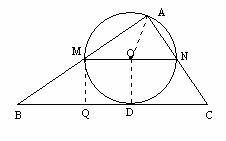 在Rt⊿ABC中,BC=
在Rt⊿ABC中,BC=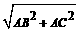 =5
=5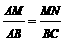 ,
,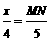 ,
,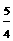 x,
∴OD=
x,
∴OD=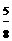 x
x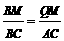 ,∴BM=
,∴BM=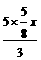 =
=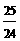 x,AB=BM+MA=
x,AB=BM+MA=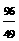
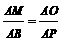 =
=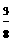 x2.
x2.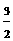
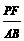 )2=
)2=
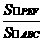
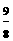 x2+6x-6
x2+6x-6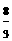 )2+2
)2+2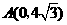 ,点
,点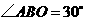 .动点
.动点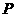 在线段
在线段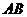 上从点
上从点 向点
向点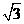 个单位的速度运动,设运动时间为
个单位的速度运动,设运动时间为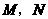 作等边
作等边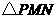 .
. 重合时
重合时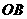 的中点
的中点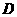 ,以
,以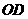 为边在
为边在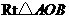 内部作如图2所示的矩形
内部作如图2所示的矩形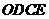 ,点
,点 秒时
秒时 .
.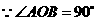 ,
,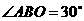 ,
,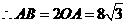 ,
,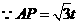 ,
, 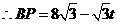 ,
,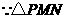 是等边三角形,
是等边三角形,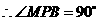 ,
,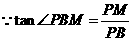 ,
,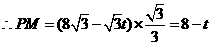 .
.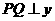 轴于
轴于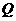 ,
,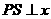 轴于
轴于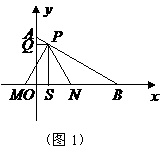 可求得
可求得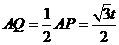 ,
,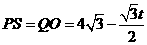 ,
,
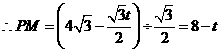 ,
, ,
,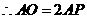 .
.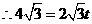 ,
,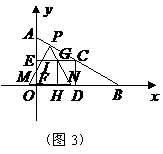
 .
.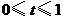 时,见图2.
时,见图2.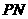 交
交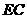 于点
于点 ,
,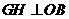 于
于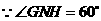 ,
,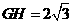 ,
,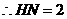 ,
,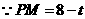 ,
,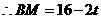 ,
,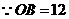 ,
,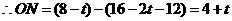 ,
,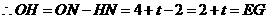 ,
,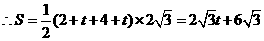 .
.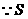 随
随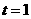 时,
时,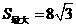 .
.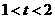 时,见图3.
时,见图3.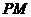 交
交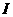 ,
,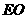 于点
于点 .
.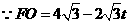 ,
,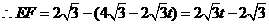 ,
,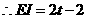 ,
,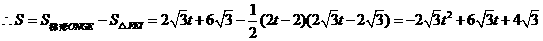 .
.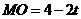 ,
,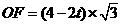 ,
,
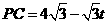 ,
,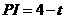 ,
,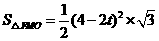
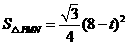 ,
,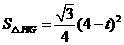
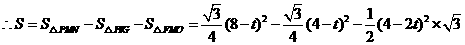
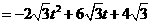 .
.
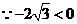 ,
,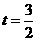 时,
时,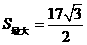 .
.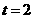 时,
时,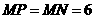 ,即
,即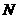 与
与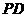 交
交 ,见图4.
,见图4.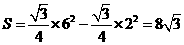 ,
,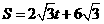 ;
;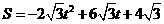 ;
;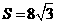 .
.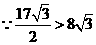 ,
,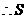 的最大值是
的最大值是 .
.