摘要：如图.二资助函数的图象经过点M. (1)求二次函数的关系式. (2)把Rt△ABC放在坐标系内.其中∠CAB = 90°.点A.B的坐标分别为.BC = 5.将△ABC沿x轴向右平移.当点C落在抛物线上时.求△ABC平移的距离. 解:在二次函数y = x2+bx+c的图象上. ∴ 解得 二次函数的关系式为y = x2-4x+1. (2)Rt△ABC中.AB = 3.BC = 5.∴AC = 4. 解得 ∵A(1.0).∴点C落在抛物线上时.△ABC向右平移个单位.
网址：http://m.1010jiajiao.com/timu3_id_454596[举报]
如图，二次函数的图象与x轴相交于A（-3，0），B（1，0）两点，与y轴相交于点C（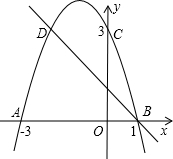
0，3），点C、D是二次函数图象上的一对对称点．一次函的图象过点B、D．
（1）求D点的坐标．
（2）求一次函数的表达式．
（3）根据图象写出使一次函数值大于二次函数值的x的取值范围． 查看习题详情和答案>>
0，3），点C、D是二次函数图象上的一对对称点．一次函的图象过点B、D．（1）求D点的坐标．
（2）求一次函数的表达式．
（3）根据图象写出使一次函数值大于二次函数值的x的取值范围． 查看习题详情和答案>>
如图，二次函数的图象与x轴相交于A、B两点，与y轴相交于点C，点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．（1）求D点的坐标；
（2）根据图象写出使一次函数值大于二次函数值的x的取值范围．
如图，二次函数的图象经过点D（0，
），且顶点C的横坐标为4，该图象在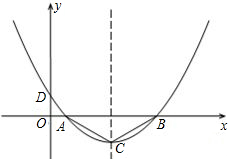
x轴上截得线段AB长为6．
（1）利用二次函数的对称性直接写出点A、B的坐标为 ；
（2）求二次函数的解析式；
（3）该抛物线的对称轴上找一点P，使PA+PD最小，求出点P的坐标；
（4）在抛物线上是否存在点Q，使△QAB与△ABC相似？如果存在，求出点Q的坐标；如果不存在，请说明理由． 查看习题详情和答案>>
| 7 |
| 9 |
| 3 |
x轴上截得线段AB长为6．（1）利用二次函数的对称性直接写出点A、B的坐标为
（2）求二次函数的解析式；
（3）该抛物线的对称轴上找一点P，使PA+PD最小，求出点P的坐标；
（4）在抛物线上是否存在点Q，使△QAB与△ABC相似？如果存在，求出点Q的坐标；如果不存在，请说明理由． 查看习题详情和答案>>
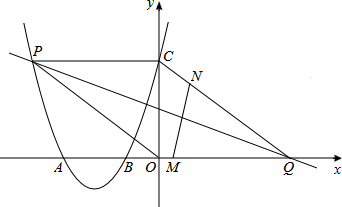
（2013•海南）如图，二次函数的图象与x轴相交于点A（-3，0）、B（-1，0），与y轴相交于点C（0，3），点P是该图象上的动点；一次函数y=kx-4k（k≠0）的图象过点P交x轴于点Q．
（1）求该二次函数的解析式；
（2）当点P的坐标为（-4，m）时，求证：∠OPC=∠AQC；
（3）点M，N分别在线段AQ、CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M，N中有一点到达Q点时，两点同时停止运动，设运动时间为t秒．连接AN，当△AMN的面积最大时，
①连接AN，当△AMN的面积最大时，求t的值；
②线段PQ能否垂直平分线段MN？若能，请求出此时点P的坐标；若不能，请说明你的理由．
查看习题详情和答案>>
（1）求该二次函数的解析式；
（2）当点P的坐标为（-4，m）时，求证：∠OPC=∠AQC；
（3）点M，N分别在线段AQ、CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M，N中有一点到达Q点时，两点同时停止运动，设运动时间为t秒．连接AN，当△AMN的面积最大时，
①连接AN，当△AMN的面积最大时，求t的值；
②线段PQ能否垂直平分线段MN？若能，请求出此时点P的坐标；若不能，请说明你的理由．
（2012•济南）如图，二次函数的图象经过（-2，-1），（1，1）两点，则下列关于此二次函数的说法正确的是（ ）