0 45283 45291 45297 45301 45307 45309 45313 45319 45321 45327 45333 45337 45339 45343 45349 45351 45357 45361 45363 45367 45369 45373 45375 45377 45378 45379 45381 45382 45383 45385 45387 45391 45393 45397 45399 45403 45409 45411 45417 45421 45423 45427 45433 45439 45441 45447 45451 45453 45459 45463 45469 45477 447348
 当x________时,式子
当x________时,式子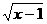 有意义. (容易题)
有意义. (容易题)