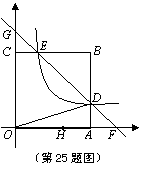
1.如图,一张边长为16㎝的正方形硬纸板,把它的四个角都剪去一个边长为x㎝的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为V㎝3,
请回答下列问题:
(1)若用含有X的代数式表示V,则V=
(2)完成下表:
|
x(㎝) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
V(㎝3) |
196 |
288 |
|
|
180 |
96 |
28 |
(3) 观察上表,容积V的值是否随x值得增大而增大?当x取什么值时,容积V的值最大?
解:
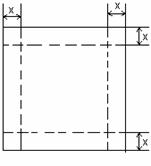
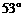 ,则秋千踏板与地面的最大距离约为多少?(参考数据:
,则秋千踏板与地面的最大距离约为多少?(参考数据: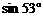 ≈0.8,
≈0.8,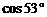 ≈0.6)
≈0.6)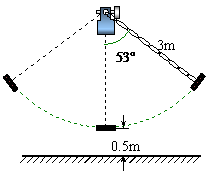
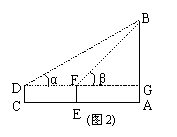
 D是AB的中点,中柱CD=1米,∠A=27°,
D是AB的中点,中柱CD=1米,∠A=27°,
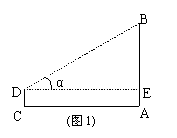 (B类)如图9,在C处用高1.20米的测角仪测得塔AB顶端B的仰角α=30º,向塔的方向前进20米到E处,又测得塔顶端B的仰角β=45°.求塔AB的高(精确到0.1米).
(B类)如图9,在C处用高1.20米的测角仪测得塔AB顶端B的仰角α=30º,向塔的方向前进20米到E处,又测得塔顶端B的仰角β=45°.求塔AB的高(精确到0.1米).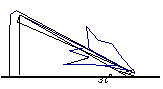 如图,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30º夹角,这棵大树在折断前的高度为
如图,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30º夹角,这棵大树在折断前的高度为
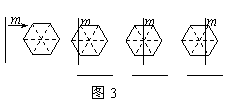
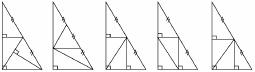
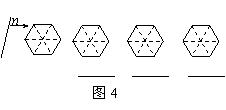 ②请你在图4中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接).
②请你在图4中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接).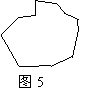
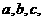 …表示;角度用
…表示;角度用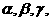 …表示);
…表示);
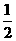 AC,延长BC到E,使CE=________,则由相似三角形得,AB=_______.
AC,延长BC到E,使CE=________,则由相似三角形得,AB=_______.
 ③.李大爷有一个边长为a的正方形鱼塘,如图,鱼塘四个角的顶点A、B、C、D上各有一棵大树。现在李大爷想把原来的鱼塘扩建成一个圆形或正方形鱼塘(原鱼塘周围的面积足够大),又不想把树挖掉(即四棵大树要在新建鱼塘的边沿上)。
③.李大爷有一个边长为a的正方形鱼塘,如图,鱼塘四个角的顶点A、B、C、D上各有一棵大树。现在李大爷想把原来的鱼塘扩建成一个圆形或正方形鱼塘(原鱼塘周围的面积足够大),又不想把树挖掉(即四棵大树要在新建鱼塘的边沿上)。