摘要: 如图.已知点A在x轴正半轴上.点A在点B的左边.α.β 是以线段AB为 斜边.顶点C在x轴上方的Rt△ABC的两个锐角. (1)若二次函数y=-x2-kx+(2+2k-k2)的图象经过A.B两点.求它的解析式, 中求出的二次函数的图象上吗?请说明理由. 解:(1)∵ α.β是Rt△ABC的两个锐角. ∴ tanα·tanβ=1.tanα>0.tanβ>0. 由题知tanα.tanβ是方程 x2+kx-(2+2k-k2)=0的两个根. ∴ tanx·tanβ=(2=2k-k2)=k2-2k-2.∴ k2-2k-2=1. 解得.k=3或k=-1. 而tanα+tanβ=-k>0. ∴ k<0.∴ k=3应舍去.k=-1. 故所求二次函数的解析式为y=-x2+x-1. (2)不在. 过C作CD⊥AB于D. 令y=0.得-x2+x-1=0. 解得x1=.x2=2. ∴ A(.0).B(2.0).AB=. ∴ tanα=.tanβ=2.设CD=m.则有CD=AD·tanα=AD. ∴ AD=2CD. 又CD=BD·tanβ=2BD. ∴ BD=CD. ∴ 2m+m=. ∴ m=.∴ AD=. ∴ C(.). 当x=时.y=≠ ∴ 点C不在(1)中求出的二次函数的图象上.
网址:http://m.1010jiajiao.com/timu3_id_454591[举报]
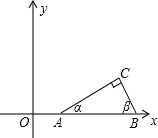 如图,已知点A(tanα,0),B(tanβ,0)在x轴正半轴上,点A在点B的左边,α、β是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角.
如图,已知点A(tanα,0),B(tanβ,0)在x轴正半轴上,点A在点B的左边,α、β是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角.(1)若二次函数y=-x2-
| 5 | 2 |
(2)点C在(1)中求出的二次函数的图象上吗?请说明理由. 查看习题详情和答案>>
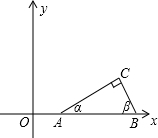 如图,已知点A(tanα,0),B(tanβ,0)在x轴正半轴上,点A在点B的左边,α、β是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角.
如图,已知点A(tanα,0),B(tanβ,0)在x轴正半轴上,点A在点B的左边,α、β是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角.
(1)若二次函数y=-x2- kx+(2+2k-k2)的图象经过A、B两点,求它的解析式;
kx+(2+2k-k2)的图象经过A、B两点,求它的解析式;
(2)点C在(1)中求出的二次函数的图象上吗?请说明理由.
查看习题详情和答案>>
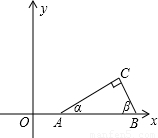 如图,已知点A(tanα,0),B(tanβ,0)在x轴正半轴上,点A在点B的左边,α、β是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角.
如图,已知点A(tanα,0),B(tanβ,0)在x轴正半轴上,点A在点B的左边,α、β是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角.(1)若二次函数y=-x2-
 kx+(2+2k-k2)的图象经过A、B两点,求它的解析式;
kx+(2+2k-k2)的图象经过A、B两点,求它的解析式;(2)点C在(1)中求出的二次函数的图象上吗?请说明理由.
查看习题详情和答案>>
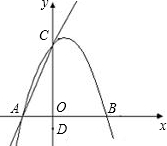 轴交于C点,且tan∠CAO=3.
轴交于C点,且tan∠CAO=3.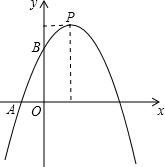 点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.
点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.