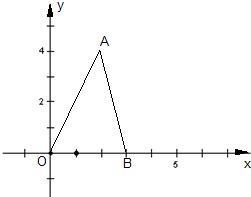
摘要:9. 如图.在平面直角坐标系中.点A.B分别在x轴.y轴上.线段OA.OB的长是方程x2-18x+72=0的两个根.点C是线段AB的中点.点D在线段OC上.OD=2CD. (1)求点C的坐标, (2)求直线AD的解析式, (3)P是直线AD上的点.在平面内是否存在点Q.使以0.A.P.Q为顶点的四边形是菱形?若存在.请直接写出点Q的坐标,若不存在.请说明理由. 解:(1)OA=6.OB=12 . 点C是线段AB的中点.OC=AC. 作CE⊥x轴于点E. ∴ OE=OA=3.CE=OB=6. ∴ 点C的坐标为(3.6). (2)作DF⊥x轴于点F △OFD∽△OEC.=.于是可求得OF=2.DF=4. ∴ 点D的坐标为(2.4). 设直线AD的解析式为y=kx+b. 把A代人得. 解得. ∴ 直线AD的解析式为y=-x+6 . (3)存在. Q1, Q2, Q3 , Q4(6.6) .
网址:http://m.1010jiajiao.com/timu3_id_454599[举报]
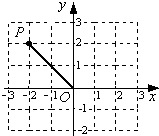
 19、如图,在平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(3,0).把△AOB沿射线OB的方向平移2个单位,其中A、O、B的对应点分别为D、E、F.
19、如图,在平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(3,0).把△AOB沿射线OB的方向平移2个单位,其中A、O、B的对应点分别为D、E、F.(1)请你画出平移后的△DEF;
(2)求线段OA在平移过程中扫过的面积.
 4、如图,在平面直角坐标系中,点P的坐标为(-2,2),将线段OP绕原点O按顺时针方向旋转
4、如图,在平面直角坐标系中,点P的坐标为(-2,2),将线段OP绕原点O按顺时针方向旋转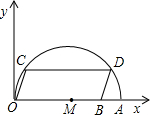 如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,求点C的坐标.
如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,求点C的坐标.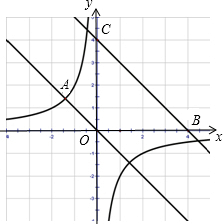 线
线 点E、F运动的时间t的值;如果不会,请说明理由.
点E、F运动的时间t的值;如果不会,请说明理由.