摘要:8.已知一次函数y=+m的图象为直线.直线绕原点O旋转180°后得直线.△ABC三个顶点的坐标分别为A(-.-1).B(.-1).C(O.2). (1)直线AC的解析式为 .直线的解析式为 , (2)如图..分别与△ABC的两边交于E.F.G.H.当m在其范围内变化时.判断四边形EFGH中有哪些量不随m的变化而变化?并简要说明理由, 中四边形EFGH的面积记为S.试求m与S的关系式.并求S的变化范围, (4)若m=1.当△ABC分别沿直线y=x与y=x平移时.判断△ABC介于直线.之间部分的面积是否改变?若不变请指出来.若改变请写出面积变化的范围. 解: (1)y= +2 y=-m (2)不变的量有: ①四边形四个内角度数不变. 理由略, ②梯形EFGH中位线长度不变.理由略. (3)S= 0<m≤1 0<s≤ (4)沿y=平移时.面积不变,沿y=x平移时.面积改变.设其面积为.则 0<≤
网址:http://m.1010jiajiao.com/timu3_id_454598[举报]
 如图,已知一次函数y=x的图象与反比例函数y=
如图,已知一次函数y=x的图象与反比例函数y=| k | x |
(1)求反比例函数的解析式;
(2)求点A的坐标;
(3)求△AOC的面积.
 阅读下面的材料:
阅读下面的材料:在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.
解答下面的问题:
(1)已知一次函数y=-2x的图象为直线l1,求过点P(1,4)且与已知直线l1平行的直线l2的函数表达式,并在坐标系中画出直线l1和l2的图象;
(2)设直线l2分别与y轴、x轴交于点A、B,过坐标原点O作OC⊥AB,垂足为C,求l1和l2两平行线之间的距离OC的长;
(3)若Q为OA上一动点,求QP+QB的最小值,并求取得最小值时Q点的坐标.
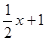 的图象与x轴交于点A.与
的图象与x轴交于点A.与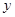 轴交于点
轴交于点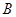 ;二次函数
;二次函数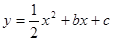 图象与一次函数y=
图象与一次函数y=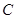 两点,与
两点,与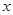 轴交于
轴交于 、
、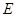 两点且
两点且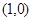
 是直角三角形?若存在,求出所有的点
是直角三角形?若存在,求出所有的点 ,若不存在,请说明理由。
,若不存在,请说明理由。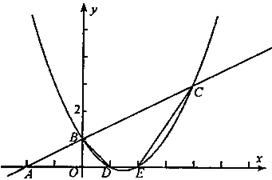



 的图象与x轴交于点A.与
的图象与x轴交于点A.与 轴交于点
轴交于点 ;二次函数
;二次函数 图象与一次函数y=
图象与一次函数y= 两点,与
两点,与 轴交于
轴交于 、
、 两点且
两点且

 是直角三角形?若存在,求出所有的点
是直角三角形?若存在,求出所有的点 ,若不存在,请说明理由。
,若不存在,请说明理由。

