摘要：(Ⅰ)证明:∵是菱形, ∴ ⊥ --------..1分 又∵ ⊥,且 ∴⊥平面, --------..3分 而AO平面 ∴⊥ ∵, ∴ ∴⊥,且 ∴⊥平面. -----5分 (Ⅱ) 取的中点.连结. ∵是等边三角形 ∴⊥ ∵⊥平面 ∴是在平面上的射影.∴由三垂线定理逆定理 可得 ∴是二面角的平面角 -----7分 ≌Rt.则.∴四边形为正方形. 在直角三角形中.. ∴== ---9分 ∴=arcsin.(或.) ∴二面角的大小是arcsin -------------10分 (Ⅱ)另解:由(Ⅰ)易证≌Rt.则. ∴四边形为正方形.以为原点.所在直线为轴. FB所在直线为轴. OA所在直线为轴.建立空间直角坐标系,则A(0.0.). B(0, ,0),C(-,0,0).=(0..-).=(-.0.-) --------------------------.7分 设=()为平面的法向量.则 ∴ .取=为平面 的一个法向量.-----8分 而=(0, ,0)为平面 的一个法向量.设为与的夹角.则==----------------------.9分 ∴二面角的大小为---------------.10分 (Ⅲ)∥, ∥平面 ∴点.到面的距离相等---------------------11分 -------------------------..12分 ----------------------14分
网址：http://m.1010jiajiao.com/timu3_id_4471614[举报]
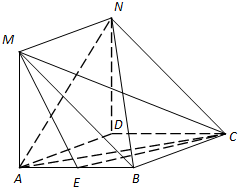（2013•武汉模拟）如图，MA⊥平面ABCD，四边形ABCD是菱形，且四边形ADNM是平行四边形．（Ⅰ）求证：AC⊥BN；
（Ⅱ）当点E在AB的什么位置时，使得AN∥平面MEC，并加以证明．
如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=a，PB=PD=| 2 |
（Ⅰ）证明PA⊥平面ABCD；
（Ⅱ）求以AC为棱，EAC与DAC为面的二面角θ的大小；
（Ⅲ）在棱PC上是否存在一点F，使BF∥平面AEC？证明你的结论． 查看习题详情和答案>>
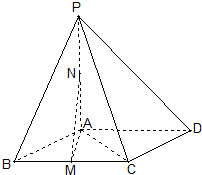如图在四棱锥P-ABCD中底面ABCD是菱形，∠ABC=60°，PA⊥平面ABCD，点M、N分别是BC、PA的中点，且PA=AB=2（1）证明：平面PBC⊥平面AMN；
（2）在线段PD上是否存在一点E，使得NM∥平面ACE；若存在，求出PE的长；若不存在，说明理由．
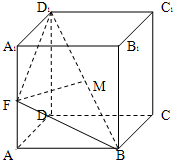如图，已知棱柱ABCD-A1B1C1D1的底面是菱形，且AA1⊥面ABCD，∠DAB=60°，AD=AA1=1，F为棱AA1的中点，M为线段BD1的中点．
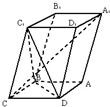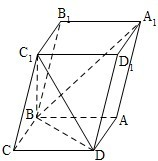
如图，已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形，且∠C1CB=∠C1CD=∠BCD=60°．