网址:http://m.1010jiajiao.com/timu3_id_4471616[举报]
2011年3月日本发生的9.0级地震引发了海啸和核泄漏。核专家为检测当地动物受核辐射后对身体健康的影响,随机选取了110只羊进行检测。其中身体健康的50只中有30只受到高度辐射,余下的60只身体不健康的羊中有10只受轻微辐射。
(1)作出2×2列联表
(2)判断有多大把握认为羊受核辐射对身体健康有影响?
【解析】本试题主要考查了列联表的运用,以及判定两个分类变量之间的相关性问题的运用首先根据题意得到2×2列联表:,然后求解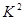 的观测值为
的观测值为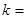
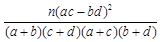
因为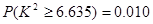 ,因此可知有99%的把握可以认为羊受核辐射对身体健康有影响。
,因此可知有99%的把握可以认为羊受核辐射对身体健康有影响。
解:(1)2×2列联表:
|
辐射程度健康类型 |
高度辐射 |
轻微辐射 |
合 计 |
|
身体健康 |
30 |
20 |
50 |
|
身体不健康 |
50 |
10 |
60 |
|
合 计 |
80 |
30 |
110 |
--------5分
-
(Ⅱ)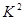 的观测值为
的观测值为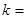
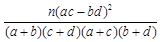
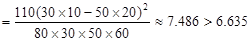 -----9分
-----9分
而 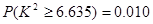
∴有99%的把握可以认为羊受核辐射对身体健康有影响。
查看习题详情和答案>>
已知函数 在
在 取得极值
取得极值
(1)求 的单调区间(用
的单调区间(用 表示);
表示);
(2)设 ,
, ,若存在
,若存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
【解析】第一问利用

根据题意 在
在 取得极值,
取得极值, 
对参数a分情况讨论,可知
当 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,

当 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,

第二问中, 由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在


从而求解。
解: 
 …..3分
…..3分
 在
在 取得极值,
取得极值,  ……………………..4分
……………………..4分
(1) 当 即
即 时 递增区间:
时 递增区间:  递减区间:
递减区间:  ,
,

当 即
即 时递增区间:
时递增区间:  递减区间:
递减区间:  ,
,
 ………….6分
………….6分
(2)  由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在

 ……………….10分
……………….10分
 , 使
, 使 成立
成立



 得:
得: 
查看习题详情和答案>>
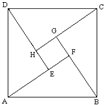
 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形.已知大正方形的面积是1,小正方形的面积是
| 1 | 25 |
(1)请根据本题题意写出sinθ与cosθ之间的等量关系,并求tanθ的值;
(2)解关于x的不等式logtanθ(x2-1)≥0.
 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小
正方形拼成的一大正方形.已知大正方形的面积是1,小正方形的面积是 .记直角三角形中的一个锐角为θ.
.记直角三角形中的一个锐角为θ.
(1)请根据本题题意写出sinθ与cosθ之间的等量关系,并求tanθ的值;
(2)解关于x的不等式logtanθ(x2-1)≥0.
查看习题详情和答案>>
根据已知条件求曲线方程的一般步骤:
(1)________:________坐标系中,用有序实数对(x,y)表示所求曲线上________M的坐标;
(2)________:寻找并写出适合题意条件p的________的集合________;
(3)________:________,列出方程f(x,y)=0;
(4)________:化方程f(x,y)=0为最简式;
(5)________:证明以化简后的方程的解为坐标的点________.
一般情况下,当化简前后方程的解是________,步骤(5)可以省略不写,若有特殊情况如增根、失根时,可适当予以说明.另外,根据情况,也可省略________,直接列出________.
查看习题详情和答案>>