0 447104 447112 447118 447122 447128 447130 447134 447140 447142 447148 447154 447158 447160 447164 447170 447172 447178 447182 447184 447188 447190 447194 447196 447198 447199 447200 447202 447203 447204 447206 447208 447212 447214 447218 447220 447224 447230 447232 447238 447242 447244 447248 447254 447260 447262 447268 447272 447274 447280 447284 447290 447298 447348
 N”的否命题是
( )
N”的否命题是
( )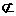 N D.
如果M∩N≠M则N
N D.
如果M∩N≠M则N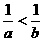
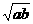 D. p:
D. p: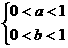 ,q:
,q: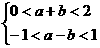
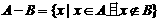 ,若
,若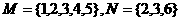 ,则N-M等于( )
,则N-M等于( )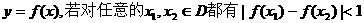 ,则称函数
,则称函数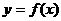 为“更生函数”,否则称“非更生函数”.函数
为“更生函数”,否则称“非更生函数”.函数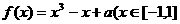 ,
,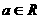 )是否为“更生函数”?如果是,请给出证明;如果不是,请说明理由.
)是否为“更生函数”?如果是,请给出证明;如果不是,请说明理由. (本小题满分12分)已知一物体做 圆周运动,出发后 t分钟内走过的路程
(本小题满分12分)已知一物体做 圆周运动,出发后 t分钟内走过的路程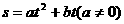 ,最初用5分钟走完第一圈,接下去用3分钟走完第二圈.
,最初用5分钟走完第一圈,接下去用3分钟走完第二圈.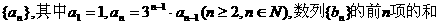
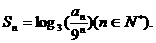 (1)求数列{an}的通项公式;(2)求数列{bn}的通项公式;
(1)求数列{an}的通项公式;(2)求数列{bn}的通项公式;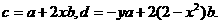 (1)当c=d时,求x,
y的值;
(1)当c=d时,求x,
y的值;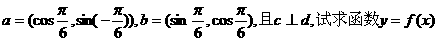 的表达式.
的表达式.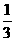 .求
.求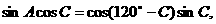 试判断△ABC的形状,并证明你的结论.
试判断△ABC的形状,并证明你的结论.